Fun with diffusion-limited aggregation

Executive Summary

My son got me interested in DLA (see intro). I made a program to draw some pretty pictures, benchmarked it (for aggregating $300\,000$ particles on a $1000 \times 1000$ canvas), profiled it and optimised it in 9 different ways to go from 8min16s to 0.686s. Along the way I explored the Maths about random walks and found useful properties that helped get the program to go faster. All the versions are available at github.com/arnodel/go-dla.

This long post tells the story of all those optimisations. I don’t think any of them is amazing, but I found it striking that I could apply so many different strategies to speed up a seemingly simple program very significantly - in fact by a factor of more than $700$ (!) Also I had a lot of fun on this journey and I feel like sharing it…

Version	Optimisation	benchmark time	github link
v1	None at all	8min16s	v1
v2	Better data structure for world map	1min35s	v1..v2
v3	Use all CPU cores	12.7s	v2..v3
v4	Remove branching on hot path	7.86s	v3..v4
v5	Do not waste a random bit	4.08s	v4..v5
v6	Precompute neighbours	2.50s	v5..v6
v7	Speed up hot path by splitting a function to inline it	2.10s	v6..v7
v8	Speed up hot path by merging two functions	1.92s	v7..v8
v9	Use the power of Maths!	0.873s	v8..v9
v10	Reduce contention on communication channel	0.687s	v9..v10

The rest of this article is composed of

• and introduction to diffusion-limiteda aggregation;
• a section for each version of the program, explaining how I dealt with the main bottleneck in the previous version and analysing the next bottleneck. There is a link to each section in the table above;
• a mathematical interlude where I explore combinatorial properties of random walks in 2D, in order to get the program to go even faster (and I get a little bit lost along the way).

What is diffusion-limited aggregation?

According to Wikipedia:

Diffusion-limited aggregation (DLA) is the process whereby particles undergoing a random walk due to Brownian motion cluster together to form aggregates of such particles.

Here is an animation to help understand what that means. The white squares are fixed particles and the red ones are in motion. They follow a Brownian motion, which is simulated here by a random walk, that is at each moment they are equally likely to move up, down, left or right. Whenever a moving particule finds itself next to a fixed particle, it becomes fixed. This way a structure slowly builds. The process started off with the horizontal line at the bottom as the “seed”. The video starts some time after that because I don’t want it to be too long!

To get an idea of the number of steps required, I display the number of aggregated particles and the total number of moves made by all the particles at any moment. You can see that it takes 100000 moves to aggregate 62 points! And this is on a tiny map of 50 by 50 squares. Imagine the number of moves required to create the image below. It was drawn on a 1000 by 1000 pixel canvas, which is 400 times bigger than the one above.

My son recently told me about DLA and showed me a program he made in Python that draws nice pictures like the one above. I thought it was very nice and decided I would write a similar program in Go. My aims were as follows.

1. Write it in Go with no with no dependencies apart from displaying graphics.
2. Show progress in real time (otherwise it’s less fun).
3. Make it as fast as I reasonably can.

For (1) I’ve decided to use Ebitengine because I’ve used it before and it’s very nice in my opinion. For (3), I’m going to use pprof. I often use it but mostly in the most basic manner, perhaps this time I can learn some more advanced features!

Version 1 - the simplest version that works

This is how it’s going to work.

• There will be an event loop that defines a channel of “pending points”. Each frame, the event loop will collect as many pending points as possible without dropping the frame rate (60 fps) and add them to the forming image.
• There will be one or more goroutines moving particles about and each time one gets stuck to the forming structure, it will send the point on the “pending points” channel and start with a new particle.
• There will be a data structure that represents the “world” with all existing points on it (and perhaps extra useful data), we will call this the “world map”.

We need to define some constants, let’s put them in constants.go:

const (
    worldWidth  = 1000
    worldHeight = 1000

    maxPendingPoints = 5000
)

I make worldWidth and worldHeight constants because I expect that they will be involved in calculations that need to be optimised. As for maxPendingPoints, I expect I won’t have to change it much. A value of 5000 seems generous, as to fill it you’d have to be able to calculate more than 5000 points every 1/60th of a second…

It will help to have a notion of Point, let’s put it in point.go:

type Point struct {
    X, Y int
}

// Move the point by one step (dir is expected to be 0, 1, 2 or 3).
func (p Point) Move(dir int) Point {
    switch dir {
    case 0:
        p.X++
    case 1:
        p.X--
    case 2:
        p.Y++
    default:
        p.Y--
    }
    return p
}

// Clamp to the point to within the confines of the world.
func (p Point) Clamp() Point {
    if p.X < 0 {
        p.X = 0
    } else if p.X >= worldWidth {
        p.X = worldWidth - 1
    }
    if p.Y < 0 {
        p.Y = 0
    } else if p.Y >= worldHeight {
        p.Y = worldHeight - 1
    }
    return p
}

// Translate the point by x and y.
func (p Point) Translate(x, y int) Point {
    return Point{X: p.X + x, Y: p.Y + y}
}

The “world map” will also be easier to manipulate if it has its own type. Let’s put it in worldmap.go:

import "iter"

type WorldMap map[Point]struct{}

// Add p to the map.
func (m WorldMap) Add(p Point) {
    m[p] = struct{}{}
}

// Contains returns true if p was added to the map.
func (m WorldMap) Contains(p Point) bool {
    _, ok := m[p]
    return ok
}

// Neighbours returns true if the map contains a point one step away from p.
func (m WorldMap) Neighbours(p Point) bool {
    return m.Contains(p.Translate(1, 0)) ||
        m.Contains(p.Translate(-1, 0)) ||
        m.Contains(p.Translate(0, 1)) ||
        m.Contains(p.Translate(0, -1))
}

// All iterates over all the points contained in the map.
func (m WorldMap) All() iter.Seq[Point] {
    return func(yield func(Point) bool) {
        for p := range m {
            if !yield(p) {
                return
            }
        }
    }
}

Next we need an event loop to draw the world. It is a type that implements the ebitengine.Game. For an intro to how that works, see the Hello, World! example. Everything happens in the Update() method, which is called every tick (1/60th of a second). This methods gets as many points from the channel of pending points as possible (until in either runs out of points or runs out of time) and draws them on the world image.

An AddPoint() method is also exposed - this is what the workers will call when one of their moving particles has aggregated. So here is game.go.

import (
    "image/color"
    "iter"
    "log"
    "runtime/pprof"
    "time"

    "github.com/hajimehoshi/ebiten/v2"
)

type Game struct {
    worldImage *ebiten.Image // We draw the world here
    pending    chan Point    // Channel where workers put points to draw
    pointCount int           // Points drawn so far
    maxPoints  int           // Total number of points to draw
    start      time.Time     // When the game started (to log timings)
}

// NewGame returns a new game where the seeds are initialPoints.
func NewGame(initialPoints iter.Seq[Point], maxPoints int) *Game {
    game := &Game{
        worldImage: ebiten.NewImage(worldWidth, worldHeight),
        pending:    make(chan Point, maxPendingPoints),
        maxPoints:  maxPoints,
    }
    for p := range initialPoints {
        game.worldImage.Set(p.X, p.Y, color.White)
    }
    game.start = time.Now()
    return game
}

// Update implements ebitengine.Game.Update().
func (g *Game) Update() error {
    var (
        i  = g.pointCount
        n  = g.maxPoints
        t0 = time.Now()
    )
    if i >= n {
        return nil
    }
    defer func() { g.pointCount = i }()
    for i%100 != 0 || time.Since(t0) < 10*time.Millisecond {
        // ^ i%100 is there so don't call time.Since(t0) too much
        select {
        case p := <-g.pending:
            // Start white and gradually fade out to black
            g.worldImage.Set(
                p.X, p.Y,
                color.Gray16{Y: uint16(0xFFFF * (n - i) / n)},
            )
            i++
            if i%1000 == 0 {
                log.Printf("Points: %d - %s", i, time.Since(g.start))
            }
            if i >= n {
                pprof.StopCPUProfile()
                return nil
            }
        default:
            return nil
        }
    }
    log.Printf("Ran out of time in Update loop after %d points", i-g.pointCount)
    return nil
}

// Draw implements ebitengine.Game.Draw().
func (g *Game) Draw(screen *ebiten.Image) {
    screen.DrawImage(g.worldImage, nil)
}

// Layout implements ebitengine.Game.Layout().
func (g *Game) Layout(outsideWidth, outsideHeight int) (int, int) {
    return worldWidth, worldHeight
}

// AddPoint adds a point to the pending points to draw.
func (g *Game) AddPoint(p Point) {
    g.pending <- p
}

All that remains to do is to have a worker that sets points in motion and detects when they get aggregated. Let’s do it the simplest way we can do it, in worker.go. Note that worldMap is a pointer, which is not required in our current implementation but may be useful if we change the WorldMap to no longer be a map. This gives us .

import (
    "log"

    "math/rand"
)

// AggregatePoints uses pickPoint to choose a starting point, moves it randomly
// until it aggregates, then registers it with addPoint.  It goes forever (or at
// least until it can no longer pick a point not on the map)
func AggregatePoints(
    worldMap *WorldMap,
    pickPoint func() Point,
    addPoint func(Point),
) {
    for {
        p := pickPoint()
        i := 0
        for worldMap.Contains(p) {
            i++
            if i == 100 {
                log.Printf("Stopping")
                return
            }
            p = pickPoint()
        }
        for !worldMap.Neighbours(p) {
            p = p.Move(rand.Intn(4)).Clamp()
        }
        worldMap.Add(p)
        addPoint(p)
    }
}

So now we can make this a Go program with a main() function putting it all together and giving us a few initialisation options. That will go in main.go.

import (
    "flag"
    "log"
    "math"
    "math/rand"
    "os"
    "runtime/pprof"

    "github.com/hajimehoshi/ebiten/v2"
)

func main() {
    var (
        cpuprofile string
        npoints    int
        methodName string
    )
    flag.StringVar(&cpuprofile, "cpuprofile", "", "write cpu profile to file")
    flag.IntVar(&npoints, "npoints", 300000, "number of points to draw")
    flag.StringVar(&methodName, "method", "circle", "method")
    flag.Parse()

    method := mustFindMethod(methodName)

    if cpuprofile != "" {
        f, err := os.Create(cpuprofile)
        if err != nil {
            log.Fatal(err)
        }
        pprof.StartCPUProfile(f)
        defer pprof.StopCPUProfile()
    }

    worldMap := &WorldMap{}

    method.init(worldMap)

    game := NewGame(worldMap.All(), npoints)

    go AggregatePoints(worldMap, method.pickPoint, game.AddPoint)

    ebiten.SetWindowSize(worldHeight, worldWidth)
    ebiten.SetWindowTitle("Diffraction-limited aggregation")
    if err := ebiten.RunGame(game); err != nil {
        log.Fatal(err)
    }
}

func mustFindMethod(name string) methodSpec {
    for _, method := range methods {
        if method.name == name {
            return method
        }
    }
    panic("invalid method")
}

// A few ways
type methodSpec struct {
    name      string          // what to call it on the command line
    init      func(*WorldMap) // function to add seeds to the world map
    pickPoint func() Point    // function to pick a random point
}

var methods = []methodSpec{
    {
        name:      "point",
        init:      DrawHorizontalPoints(1),
        pickPoint: RandomPoint,
    },
    {
        name:      "point2",
        init:      DrawHorizontalPoints(2),
        pickPoint: RandomPoint,
    },
    {
        name:      "circle",
        init:      DrawCircle,
        pickPoint: RandomPointInCircle,
    },
    {
        name:      "hline",
        init:      DrawHorizontalLine,
        pickPoint: RandomPoint,
    },
}

func RandomPointInCircle() Point {
    a := rand.Float64() * math.Pi * 2
    r := math.Sqrt(rand.Float64()) * worldWidth / 2
    return Point{
        X: worldWidth/2 + int(math.Cos(a)*r),
        Y: worldHeight/2 + int(math.Sin(a)*r),
    }
}

func RandomPoint() Point {
    return Point{
        X: rand.Intn(worldWidth),
        Y: rand.Intn(worldHeight),
    }
}

func DrawHorizontalLine(m *WorldMap) {
    for x := 0; x < worldWidth; x++ {
        m.Add(Point{X: x, Y: worldHeight / 2})
    }
}

func DrawHorizontalPoints(nPoints int) func(*WorldMap) {
    return func(m *WorldMap) {
        for i := 1; i <= nPoints; i++ {
            m.Add(Point{X: i * worldWidth / (nPoints + 1), Y: worldHeight / 2})
        }
    }
}

func DrawCircle(m *WorldMap) {
    const N = 2000
    for i := 0; i < N; i++ {
        a := math.Pi * 2 * float64(i) / N
        m.Add(Point{
            X: int(worldWidth / 2 * (1 + math.Cos(a))),
            Y: int(worldHeight / 2 * (1 + math.Sin(a))),
        }.Clamp())
    }
}

Let’s try it!

❯ go run . -cpuprofile v1.pprof
2024/10/14 17:26:59 Points: 1000 - 11.427302834s
2024/10/14 17:27:10 Points: 2000 - 22.592300917s
2024/10/14 17:27:20 Points: 3000 - 33.275559625s
2024/10/14 17:27:31 Points: 4000 - 43.320070125s
[...]
2024/10/14 17:35:04 Points: 297000 - 8m16.458362959s
2024/10/14 17:35:04 Points: 298000 - 8m16.475744584s
2024/10/14 17:35:04 Points: 299000 - 8m16.475820375s
2024/10/14 17:35:04 Points: 300000 - 8m16.475883084s

It took more than 8 minutes to draw 300000 points, but we get a nice picture in the end.

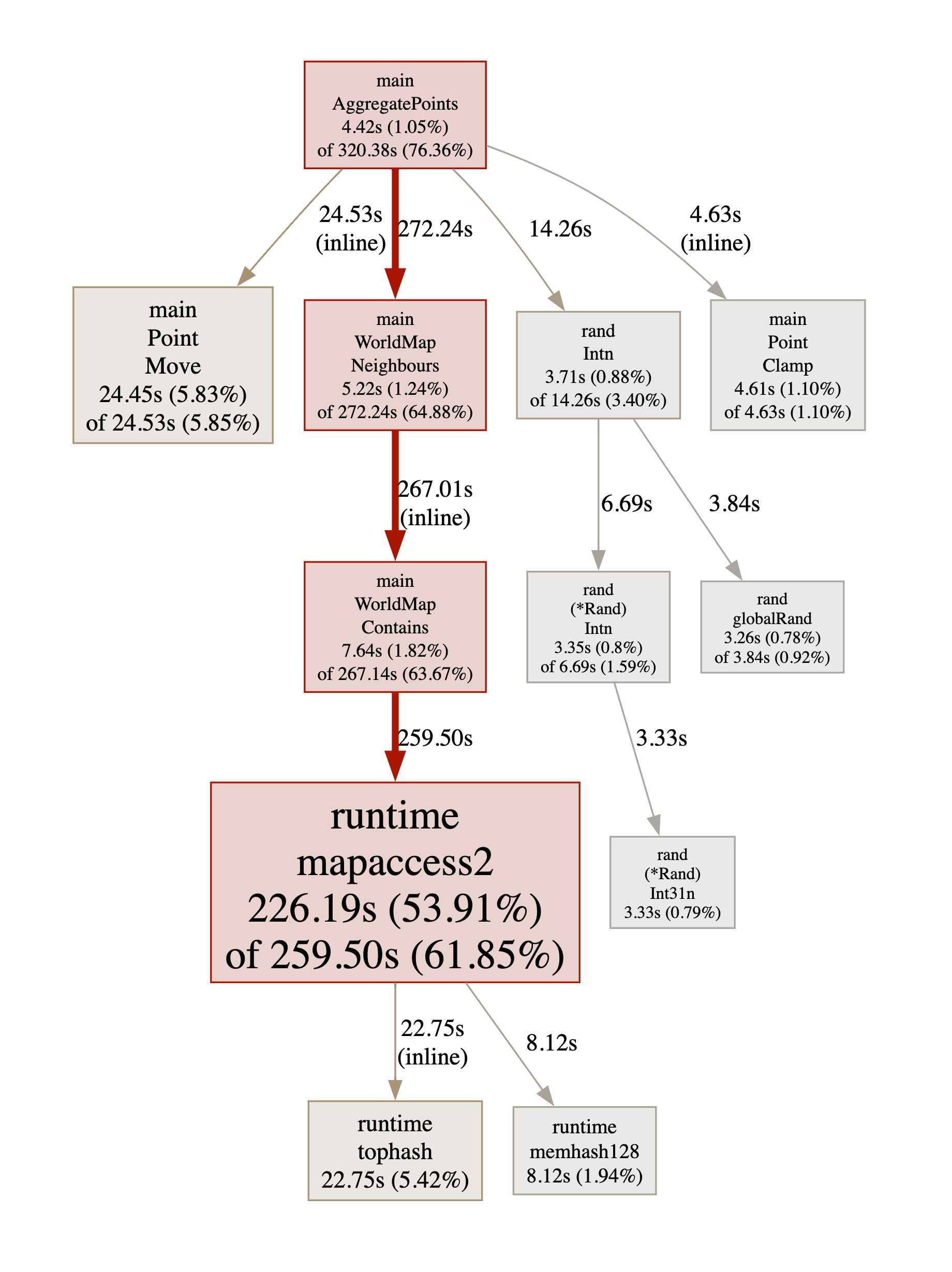
Let’s see what took so long (I have slightly edited the result to focus on the relevant information).

 ❯ go tool pprof -http :8000 v1.pprof
Serving web UI on http://localhost:8000

Obviously, using a map to implement WorldMap wasn’t very judicious. By the way, another way to get this information in text form would have been as follows.

❯ go tool pprof v1.pprof
File: go-dla
Type: cpu
Time: Oct 14, 2024 at 7:43pm (BST)
Duration: 483.16s, Total samples = 419.59s (86.84%)
Entering interactive mode (type "help" for commands, "o" for options)
(pprof) top 5
Showing nodes accounting for 322.67s, 76.90% of 419.59s total
Dropped 240 nodes (cum <= 2.10s)
Showing top 5 nodes out of 55
      flat  flat%   sum%        cum   cum%
   226.19s 53.91% 53.91%    280.24s 66.79%  runtime.mapaccess2
    31.24s  7.45% 61.35%     31.24s  7.45%  runtime.pthread_cond_signal
    24.45s  5.83% 67.18%     24.53s  5.85%  main.Point.Move
    22.75s  5.42% 72.60%     22.75s  5.42%  runtime.tophash (inline)
    18.04s  4.30% 76.90%     18.04s  4.30%  runtime.pthread_cond_wait
(pprof) 

Version 2 - Array-backed WorldMap

The obvious change to try here is to use a slice or an array as the backing data structure for WorldMap. Since the dimensions of the world are known at compile time, let’s use an array. So worldmap.go becomes this:

import "iter"

type WorldMap [worldWidth * worldHeight]bool

// Add p to the map.
func (m *WorldMap) Add(p Point) {
    if p.X < 0 || p.X >= worldWidth || p.Y < 0 || p.Y >= worldHeight {
        return
    }
    m[p.X*worldHeight+p.Y] = true
}

// Contains returns true if p was added to the map.
func (m *WorldMap) Contains(p Point) bool {
    if p.X < 0 || p.X >= worldWidth || p.Y < 0 || p.Y >= worldHeight {
        return false
    }
    return m[p.X*worldHeight+p.Y]
}

// Neighbours returns true if the map contains a point one step away from p.
func (m *WorldMap) Neighbours(p Point) bool {
    return m.Contains(p.Translate(1, 0)) ||
        m.Contains(p.Translate(-1, 0)) ||
        m.Contains(p.Translate(0, 1)) ||
        m.Contains(p.Translate(0, -1))
}

// All iterates over all the points contained in the map.
func (m *WorldMap) All() iter.Seq[Point] {
    return func(yield func(Point) bool) {
        for i, added := range m {
            if added {
                p := Point{X: i / worldHeight, Y: i % worldHeight}
                if !yield(p) {
                    return
                }
            }
        }
    }
}

Let’s try it.

❯ go run . -cpuprofile v2.pprof
2024/10/14 20:14:11 Points: 1000 - 2.131455708s
2024/10/14 20:14:13 Points: 2000 - 4.114867083s
2024/10/14 20:14:15 Points: 3000 - 6.18145s
2024/10/14 20:14:17 Points: 4000 - 8.198248458s
[...]
2024/10/14 20:15:45 Points: 297000 - 1m35.633048875s
2024/10/14 20:15:45 Points: 298000 - 1m35.633134708s
2024/10/14 20:15:45 Points: 299000 - 1m35.633231291s
2024/10/14 20:15:45 Points: 300000 - 1m35.650491083s

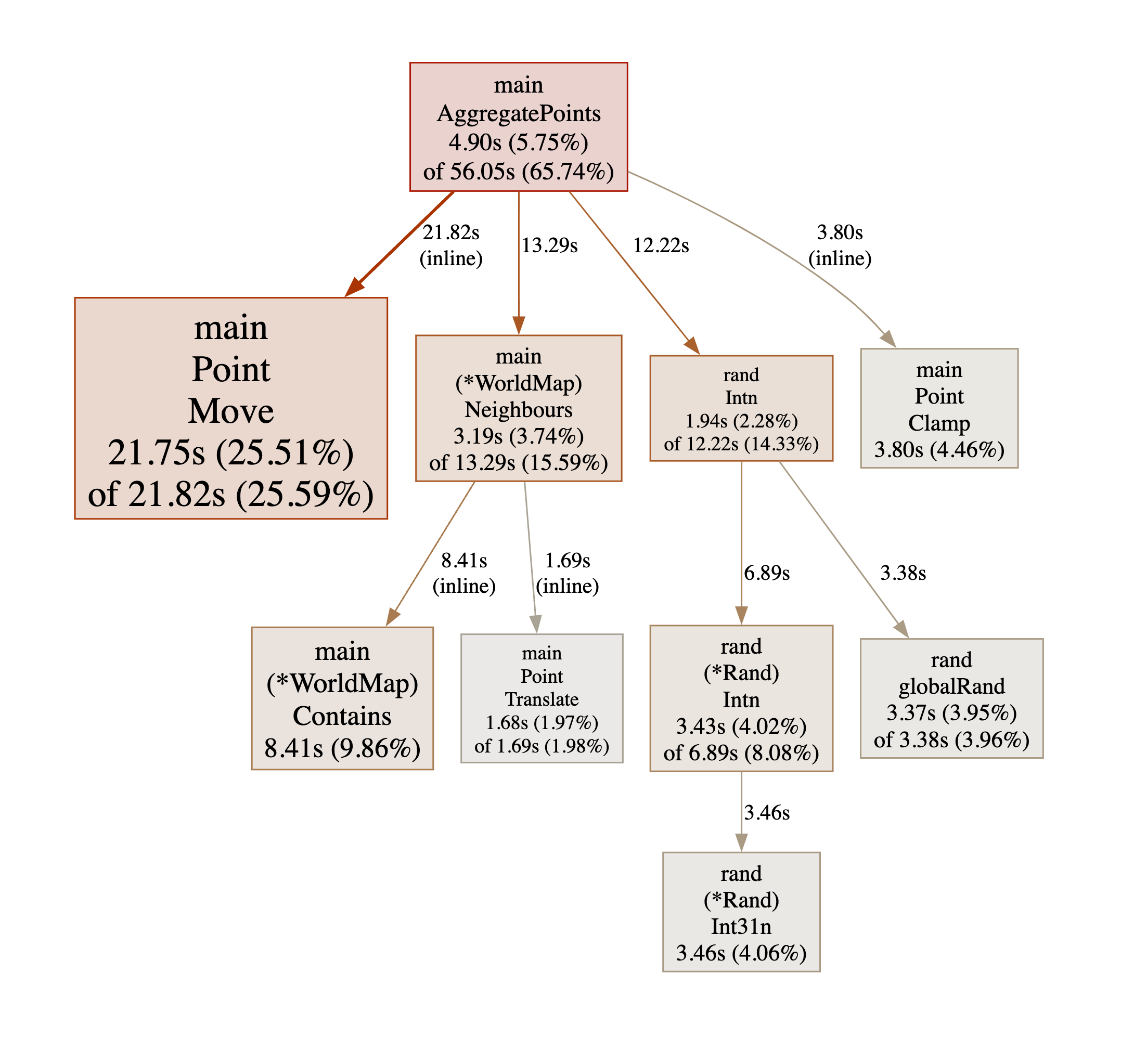
The result is just as pretty than version 1, we get it 5 times faster! Wow that was easy, but let’s see what the next bottleneck is (again I have removed irrelevant nodes from the result).

❯ go tool pprof -http :8000 v2.pprof

As for version 1, it’s even more obvious using the CLI. Note we can also bring up a listing of the offending function with some stats about each line.

❯ go tool pprof v2.pprof
File: go-dla
Type: cpu
Time: Oct 14, 2024 at 8:22pm (BST)
Duration: 95.70s, Total samples = 85.26s (89.09%)
Entering interactive mode (type "help" for commands, "o" for options)
(pprof) top 5
Showing nodes accounting for 48.77s, 57.20% of 85.26s total
Dropped 137 nodes (cum <= 0.43s)
Showing top 5 nodes out of 53
      flat  flat%   sum%        cum   cum%
    21.75s 25.51% 25.51%     21.82s 25.59%  main.Point.Move (inline)
     8.41s  9.86% 35.37%      8.41s  9.86%  main.(*WorldMap).Contains (inline)
     8.17s  9.58% 44.96%      8.17s  9.58%  internal/chacha8rand.block
     5.54s  6.50% 51.45%      5.54s  6.50%  runtime.pthread_cond_signal
     4.90s  5.75% 57.20%     65.77s 77.14%  main.AggregatePoints
(pprof) list main.Point.Move
Total: 85.26s
ROUTINE ======================== main.Point.Move in /Users/arno/Personal/Projects/go-dla/point.go
    21.75s     21.82s (flat, cum) 25.59% of Total
         .          .      8:func (p Point) Move(dir int) Point {
         .          .      9:   switch dir {
     5.06s      5.06s     10:   case 0:
     4.88s      4.92s     11:           p.X++
     1.15s      1.15s     12:   case 1:
     5.03s      5.04s     13:           p.X--
     790ms      790ms     14:   case 2:
     2.40s      2.41s     15:           p.Y++
         .          .     16:   default:
     2.44s      2.45s     17:           p.Y--
         .          .     18:   }
         .          .     19:   return p
         .          .     20:}
         .          .     21:
         .          .     22:// Clamp to the point to within the confines of the world

The function is obviously in the hot path, as the main job of the program is to move a point around until it can be aggregated. It’s already inlined as pprof tells us. It takes a lot more time than other functions on the hot path (such as WorldMap.Contains() or WorldMap.Neighbours()) and it is very simple. However it has a fair amount of branching (one for each case), and I hear that modern CPUs don’t like branching because it messes with their instruction pipeline so there may be scope for improvement here. But before we do that, there is an obvious thing that modern processors can do well and we haven’t tried yet: parallelism. I think we should parallelise first, because

• it’s likely to bring a very significant speedup; and
• it might turn out that the biggest bottleneck after parallelising is something altogether completely different.

Version 3 - Parallel workers

This is going to be an easy adjustment. Essentially, instead of spawning one worker goroutine at the start, we will spawn N, N being the number of “cores” in the processor (to find that out we will use runtime.GOMAXPROCS()).

Changes to AggregatePoints() in worker.go are limited to adding a new function parameter workerNumber int just so that we can specify which worker is logging a message.

Changes to main() in main.go are just to

• have a new CLI argument so the number of workers can be adjusted and
• spawn N worker goroutines rather than just one.

This is probably best expressed as a diff:

diff --git a/main.go b/main.go
index b3a8b02..63f2bb1 100644
--- a/main.go
+++ b/main.go
@@ -6,6 +6,7 @@ import (
     "math"
     "math/rand"
     "os"
+	"runtime"
     "runtime/pprof"
 
     "github.com/hajimehoshi/ebiten/v2"
@@ -13,16 +14,25 @@ import (
 
 func main() {
     var (
-		cpuprofile string
-		npoints    int
-		methodName string
+		cpuprofile  string
+		npoints     int
+		methodName  string
+		workerCount int
     )
     flag.StringVar(&cpuprofile, "cpuprofile", "", "write cpu profile to file")
     flag.IntVar(&npoints, "npoints", 300000, "number of points to draw")
     flag.StringVar(&methodName, "method", "circle", "method")
+	flag.IntVar(&workerCount, "workers", 0, "number of workers (if < 0, add GOMAXPROCS)")
     flag.Parse()
 
     method := mustFindMethod(methodName)
+	if workerCount <= 0 {
+		workerCount += runtime.GOMAXPROCS(0)
+	}
+	if workerCount <= 0 {
+		workerCount = 1
+	}
+	log.Printf("Worker count: %d", workerCount)
 
     if cpuprofile != "" {
         f, err := os.Create(cpuprofile)
@@ -39,7 +49,9 @@ func main() {
 
     game := NewGame(worldMap.All(), npoints)
 
-	go AggregatePoints(worldMap, method.pickPoint, game.AddPoint)
+	for i := 1; i <= workerCount; i++ {
+		go AggregatePoints(i, worldMap, method.pickPoint, game.AddPoint)
+	}
 
     ebiten.SetWindowSize(worldHeight, worldWidth)
     ebiten.SetWindowTitle("Diffraction-limited aggregation")
diff --git a/worker.go b/worker.go
index 43abfc6..6a8068a 100644
--- a/worker.go
+++ b/worker.go
@@ -10,6 +10,7 @@ import (
 // until it aggregates, then registers it with addPoint.  It goes forever (or at
 // least until it can no longer pick a point not on the map)
 func AggregatePoints(
+	workerNumber int,
     worldMap *WorldMap,
     pickPoint func() Point,
     addPoint func(Point),
@@ -20,7 +21,7 @@ func AggregatePoints(
         for worldMap.Contains(p) {
             i++
             if i == 100 {
-				log.Printf("Stopping")
+				log.Printf("Worker %d stopping", workerNumber)
                 return
             }
             p = pickPoint()

Or you can see the new versions of main.go and worker.go on github.

Let’s try it!

❯ go run . -cpuprofile v3.pprof
2024/10/14 21:44:55 Worker count: 10
2024/10/14 21:44:56 Points: 1000 - 326.773875ms
2024/10/14 21:44:56 Points: 2000 - 608.128792ms
2024/10/14 21:44:56 Points: 3000 - 873.241917ms
2024/10/14 21:44:56 Points: 4000 - 1.13847325s
[...]
2024/10/14 21:45:08 Points: 173000 - 12.595318125s
2024/10/14 21:45:08 Points: 174000 - 12.598245208s
2024/10/14 21:45:08 Ran out of time in Update loop after 6304 points
2024/10/14 21:45:08 Points: 175000 - 12.6055255s
[...]
2024/10/14 21:45:08 Points: 212000 - 12.665401792s
2024/10/14 21:45:08 Ran out of time in Update loop after 13663 points
2024/10/14 21:45:08 Points: 213000 - 12.672544875s
[...]
2024/10/14 21:45:08 Points: 225000 - 12.681567458s
2024/10/14 21:45:08 Ran out of time in Update loop after 13300 points
2024/10/14 21:45:08 Points: 226000 - 12.68903025s
[...]
2024/10/14 21:45:08 Points: 240000 - 12.698756958s
2024/10/14 21:45:08 Ran out of time in Update loop after 14900 points
2024/10/14 21:45:08 Points: 241000 - 12.70546875s
[...]
2024/10/14 21:45:08 Points: 256000 - 12.714714625s
2024/10/14 21:45:08 Ran out of time in Update loop after 16500 points
2024/10/14 21:45:08 Points: 257000 - 12.721866s
[...]
2024/10/14 21:45:08 Points: 272000 - 12.731554375s
2024/10/14 21:45:08 Ran out of time in Update loop after 15700 points
2024/10/14 21:45:08 Points: 273000 - 12.738769667s
[...]
2024/10/14 21:45:08 Points: 290000 - 12.748475042s
2024/10/14 21:45:08 Ran out of time in Update loop after 17700 points
2024/10/14 21:45:08 Points: 291000 - 12.755820708s
[...]
2024/10/14 21:45:08 Points: 297000 - 12.759201583s
2024/10/14 21:45:08 Points: 298000 - 12.7597945s
2024/10/14 21:45:08 Points: 299000 - 12.760386167s
2024/10/14 21:45:08 Points: 300000 - 12.761009083s

So version 3 is faster than version 2 by a factor of 7.5! That’s pretty good, and not very surprising as on my machine I was runnning 10 workers and they were probably able to each have their own core to work on. However, there are two things to note straight away.

1. As the logs show, the Update() function wasn’t able to consume all available points a few times (but mainly towards the end). It’s probably OK as the more points are already on the graph, the shorter the path a new particle needs to walk before aggregating. So towards the end the points keep coming fast and the event loop needs to stop consuming them from time to time to redraw the screen.
2. WorldMap is not thread-safe, and is concurrently accessed by all the workers. I think that’s OK too, because the only changes to values in the array are from false to true, so the worse that can happen is that a worker will add a point on the map when there is already one. That is probably very unlikely anyway, as there are 10 workers (so there are only 10 particles in motion at one time) and the world has 1000*1000 locations where points can be added.

Let’s also check the CPU profile to see if Point.Move() is still the main bottleneck as in version 2.

❯ go tool pprof v3.pprof
File: go-dla-v2
Type: cpu
Time: Oct 14, 2024 at 9:44pm (BST)
Duration: 12.87s, Total samples = 92.22s (716.55%)
Entering interactive mode (type "help" for commands, "o" for options)
(pprof) top 5
Showing nodes accounting for 55.89s, 60.61% of 92.22s total
Dropped 168 nodes (cum <= 0.46s)
Showing top 5 nodes out of 52
      flat  flat%   sum%        cum   cum%
    26.08s 28.28% 28.28%     26.19s 28.40%  main.Point.Move (inline)
     9.80s 10.63% 38.91%      9.82s 10.65%  main.(*WorldMap).Contains (inline)
     9.31s 10.10% 49.00%      9.31s 10.10%  internal/chacha8rand.block
     5.53s  6.00% 55.00%     78.32s 84.93%  main.AggregatePoints
     5.17s  5.61% 60.61%      5.20s  5.64%  main.Point.Clamp (inline)
(pprof) 

In fact the results are very similar to version 2, where all the calculations happened in a single core. That makes sense as the timings for each goroutine are added. So in version 3, 10 goroutines spent a total time of 26,08s in Point.Move(), and in version 3, one goroutine spent 21.75s in the same function. I am not sure what explains the difference (perhaps the fact that other tasks on my computer also need CPU time!).

So now that we have made sure that we use all the cores on the machine, let’s see if we can optimise this bottleneck.

Version 4 - Branchless Point.Move()

So we have this method in point.go:

// Move the point by one step (dir is expected to be 0, 1, 2 or 3).
func (p Point) Move(dir int) Point {
    switch dir {
    case 0:
        p.X++
    case 1:
        p.X--
    case 2:
        p.Y++
    default:
        p.Y--
    }
    return p
}

Given how switch is implemented in Go, this means there are probably going to be 3 conditional branches. Let’s try to check that! There are several ways we could do it, but since I’m trying to get better at using pprof I’m going to use one of its features. First of all, as we saw before, Point.Move() is currently inlined in the binary, which makes it a bit harder to locate. So I’m going to tell the go compiler not to inline it:

//go:noline
func (p Point) Move(dir int) Point {
    switch dir {
    ...

Then I can make a build of it, run it and examine the CPU profile with pprof. Note that I need to do an explicit build step instead of using go run .. I think the reason is that with go run . the binary gets deleted straight after the run, so pprof is unable to find the symbol table

❯ go build -o go-dla-v3-noinline
❯ ./go-dla-v3-noinline -cpuprofile v3-noinline.pprof 2>& /dev/null
❯ go tool pprof v3-noinline.pprof
File: go-dla-v3-noinline
Type: cpu
Time: Oct 14, 2024 at 10:44pm (BST)
Duration: 12.94s, Total samples = 93.10s (719.36%)
Entering interactive mode (type "help" for commands, "o" for options)
(pprof) disasm Point.Move
Total: 93.10s
ROUTINE ======================== main.Point.Move
 29.53s     29.70s (flat, cum) 31.90% of Total
  1.55s      1.55s  100268110: CBNZ R2, 3(PC)     ;main.Point.Move point.go:12
  7.44s      7.47s  100268114: ADD $1, R0, R0     ;main.Point.Move point.go:13
      .          .  100268118: JMP 10(PC)         ;point.go:13
  860ms      870ms  10026811c: CMP $1, R2         ;main.Point.Move point.go:14
      .          .  100268120: BNE 3(PC)          ;point.go:14
  7.28s      7.34s  100268124: SUB $1, R0, R0     ;main.Point.Move point.go:15
      .          .  100268128: JMP 6(PC)          ;point.go:15
  1.48s      1.49s  10026812c: CMP $2, R2         ;main.Point.Move point.go:16
      .          .  100268130: BNE 3(PC)          ;point.go:16
  3.81s      3.83s  100268134: ADD $1, R1, R1     ;main.Point.Move point.go:17
      .          .  100268138: JMP 2(PC)          ;point.go:17
  4.02s      4.04s  10026813c: SUB $1, R1, R1     ;main.Point.Move point.go:19
  3.09s      3.11s  100268140: RET                ;main.Point.Move point.go:21
      .          .  100268144: ?                  ;point.go:21
      .          .  100268148: ?
      .          .  10026814c: ?
(pprof)

As expected, we can see

• 3 conditional jumps: one instance of CBNZ (for case 0) and two of BNE (for case 1 and case 2)
• 3 plains jumps, to break out of the first 3 switch cases.

So let’s see if Point.Move(dir int) can be improved. It takes dir which between 0 and 3, really 2 bits a and b, which we could write as

    a := dir & 1
    b := dir >> 1

Now let’s compute $x = a - b$ and $y = a + b - 1$ for all the values of $a$ and $b$

$a$	$b$	$x = a - b$	$y = a + b - 1$	$(p.X + x, p.Y + y)$
$0$	$0$	$0$	$-1$	$(p.X, p.Y - 1)$
$1$	$0$	$1$	$0$	$(p.X + 1, p.Y)$
$0$	$1$	$-1$	$0$	$(p.X - 1, p.Y)$
$1$	$1$	$0$	$1$	$(p.X, p.Y + 1)$

The last column in the table above shows us that we can move p by one step in exactly one direction as follows

func (p Point) Move(dir int) Point {
    a := dir & 1
    b := dir >> 1
    return Point{
        X: p.X + a - b,
        Y: p.Y + a + b - 1,
    }
}

Let’s try it (from now on I will not worry about when Update runs out of time, unless it happens too much).

❯ go run . -cpuprofile v4.pprof
2024/10/14 22:25:17 Worker count: 10
2024/10/14 22:25:17 Points: 1000 - 188.212041ms
2024/10/14 22:25:17 Points: 2000 - 378.719291ms
2024/10/14 22:25:17 Points: 3000 - 537.259583ms
2024/10/14 22:25:18 Points: 4000 - 706.399958ms
[...]
2024/10/14 22:25:25 Points: 297000 - 7.684472125s
2024/10/14 22:25:25 Points: 298000 - 7.685051333s
2024/10/14 22:25:25 Points: 299000 - 7.685599583s
2024/10/14 22:25:25 Points: 300000 - 7.686393666s

This worked really well! Version 4 is 1.9 times faster than version 3. Out of interest, let’s see what the new Point.Move() method compiles to using pprof and what time is spent in it compared with v3. For this, as for v3, I will make a version of Point.Move() with the //go:noinline annotation.

❯ go build -o go-dla-v4-noinline
❯ ./go-dla-v4-noinline -cpuprofile v4-noinline.pprof 2>& /dev/null
❯ go tool pprof v4-noinline.pprof
File: go-dla-v4-noinline
Type: cpu
Time: Oct 14, 2024 at 11:22pm (BST)
Duration: 8.37s, Total samples = 60.06s (717.77%)
Entering interactive mode (type "help" for commands, "o" for options)
(pprof) disasm Point.Move
Total: 60.06s
ROUTINE ======================== main.Point.Move
 1.52s      1.53s (flat, cum)  2.55% of Total
 1.52s      1.53s  100268130: AND $1, R2, R3       ;main.Point.Move point.go:11
     .          .  100268134: ADD R0, R3, R4       ;point.go:14
     .          .  100268138: SUB R2->1, R4, R0
     .          .  10026813c: ADD R1, R3, R3       ;point.go:15
     .          .  100268140: ADD R2->1, R3, R2
     .          .  100268144: SUB $1, R2, R1
     .          .  100268148: RET                  ;point.go:13
     .          .  10026814c: ?
(pprof) 

That is 1.52s spent altogether in Point.Move, compare with version 3 that was 29.53s! I have heard about the impact of incorrect branch prediction before, but it seems to me that I’m seeing a probably very simple but striking example of this phenomenon. In our case, dir is random so the branch predictor must be completely useless. Removing the branches altogether seems to speed up this function by a factor of about 20!

All very nice but what’s the next bottleneck?

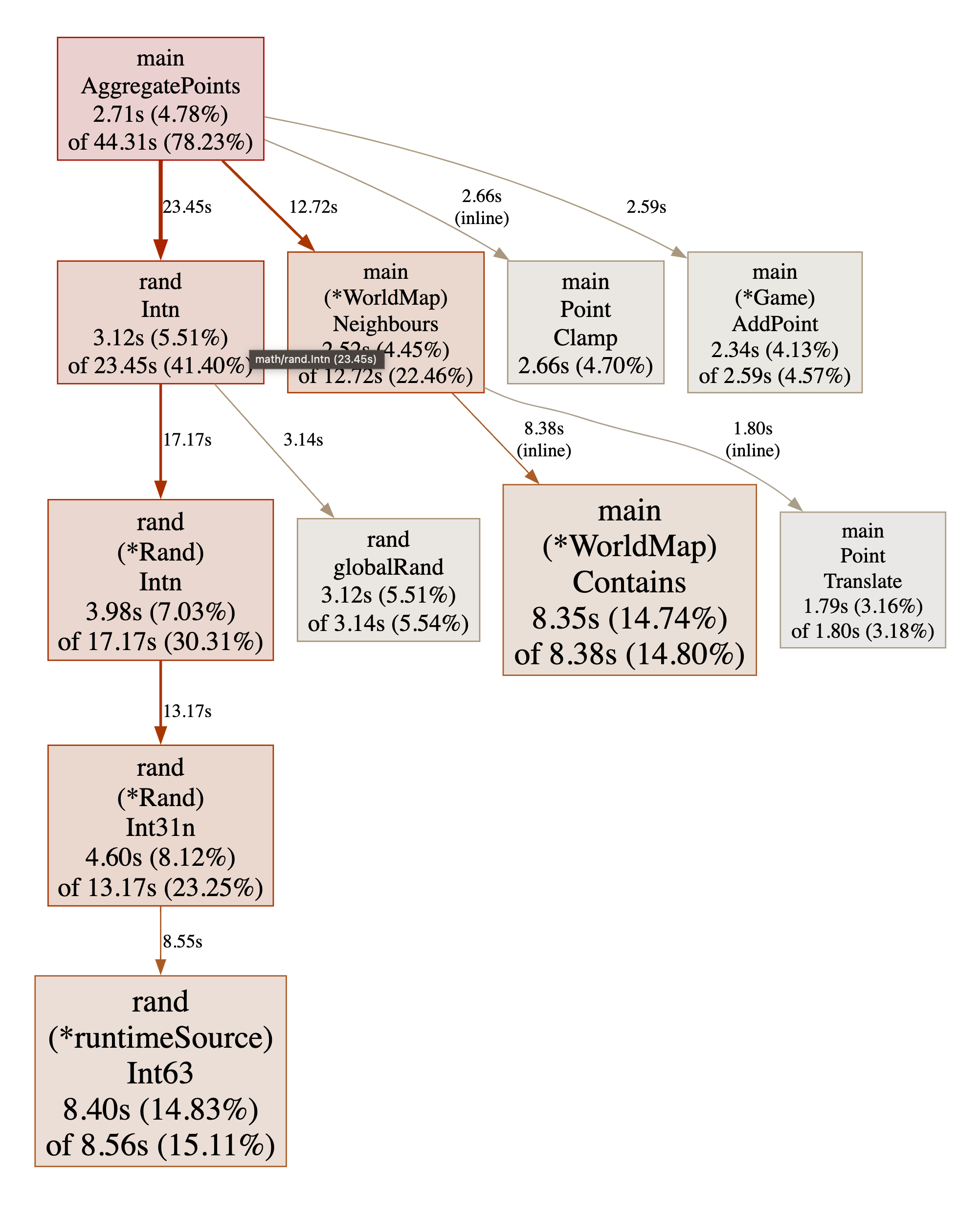
❯ go tool pprof -http :8000 v4.pprof
Serving web UI on http://localhost:8000

As previously I’ve trimmed off the irrelevant parts:

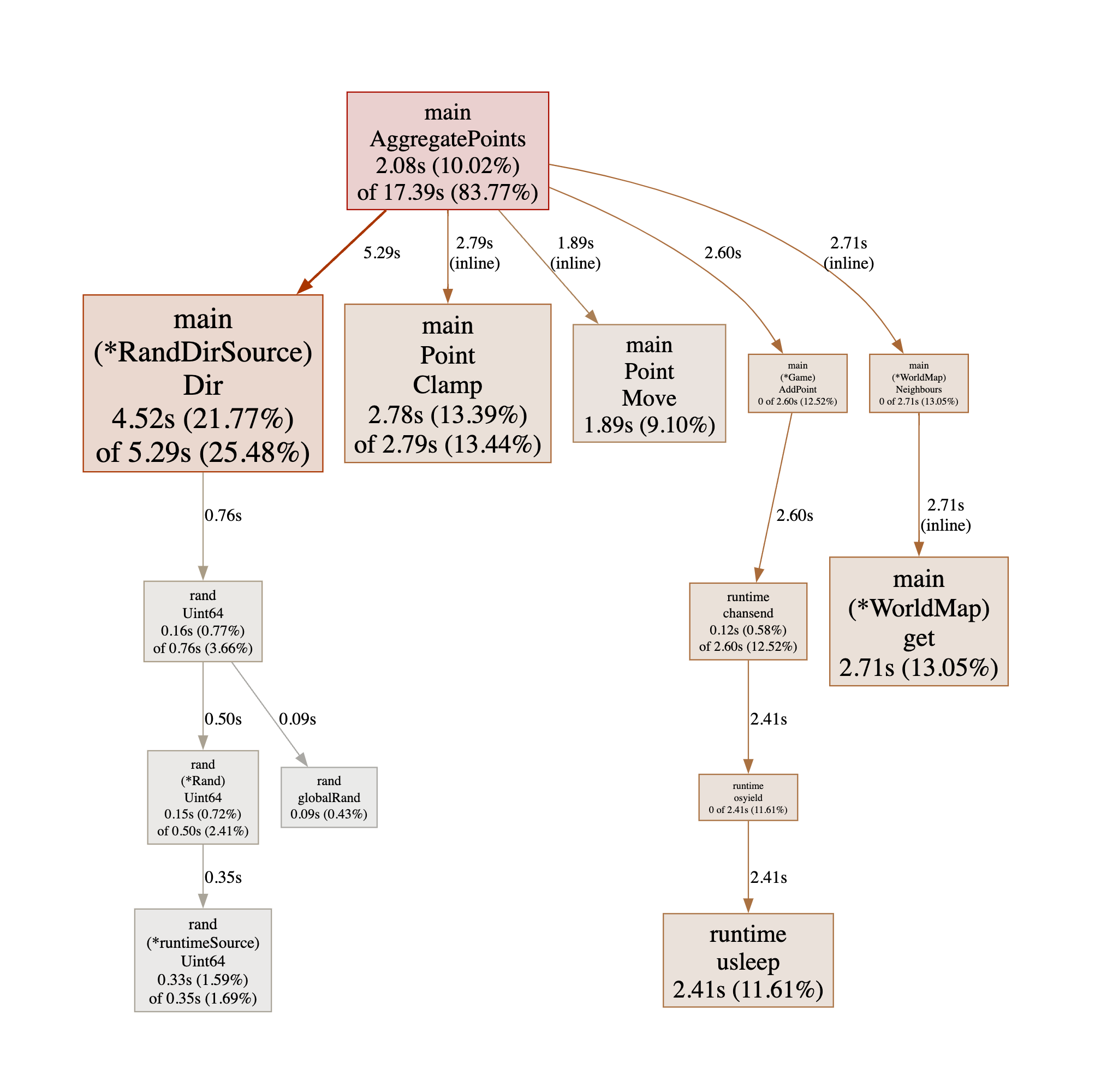
There is clearly something going on with generating random numbers.

Version 5 - Stop wasting random numbers

Let’s look more closely at random number generation in AggregatePoints:

        for !worldMap.Neighbours(p) {
            p = p.Move(rand.Intn(4)).Clamp()
        }

Every time we draw a random number to chose a direction for a random walk, that requires only 2 random bits for a direction but we generate 64. And the graph above tells us that this random number generation is the main bottleneck in our program.

That means we are being very wasteful with the precious resource that is random bits! Every time we need 2, we make 64 and throw away 62. Surely we can slightly rework this code so that it finishes off all the random bits it asks for. Something like this

type RandDirSource struct {
    r uint64
    i int
}

func (s *RandDirSource) Dir() int {
    if s.i == 0 {
        s.i = 32
        s.r = rand.Uint64()
    }
    dir := int(s.r % 4)
    s.i--
    s.r >>= 2
    return dir
}

if r is a *RandomDirSource, r.Dir() gives you an int containing 2 random bits, but keeps hold of the remaning random bits it asks for. This way you can ask r for a random direction 32 times before it needs to generate a new 64 bit random number! Let’s make AggregatePoints() use it insteand of rand.Intn(4):

func AggregatePoints(
    workerNumber int,
    worldMap *WorldMap,
    pickPoint func() Point,
    addPoint func(Point),
) {
    var randDirSrc RandDirSource
    for {
        p := pickPoint()
        i := 0
        for worldMap.Contains(p) {
            i++
            if i == 100 {
                log.Printf("Worker %d stopping", workerNumber)
                return
            }
            p = pickPoint()
        }
        for !worldMap.Neighbours(p) {
            p = p.Move(randDirSrc.Dir()).Clamp()
        }
        worldMap.Add(p)
        addPoint(p)
    }
}

❯ go run . -cpuprofile v5.pprof
2024/10/15 20:30:28 Worker count: 10
2024/10/15 20:30:28 Points: 1000 - 146.306ms
2024/10/15 20:30:28 Points: 2000 - 202.060042ms
2024/10/15 20:30:28 Points: 3000 - 315.281834ms
2024/10/15 20:30:28 Points: 4000 - 403.433167ms
[...]
2024/10/15 20:30:32 Points: 297000 - 4.080072375s
2024/10/15 20:30:32 Points: 298000 - 4.08042025s
2024/10/15 20:30:32 Points: 299000 - 4.080882167s
2024/10/15 20:30:32 Points: 300000 - 4.08144575s

We’ve increased the speed of our program by another factor of 1.9. It’s quite exciting that after four rounds of optimisation, we can still easily find some substantial improvements… So let’s not stop here! The previous pprof graph hinted that the next bottleneck was going WorldMap.Neighbours() but let’s check.

❯ go tool pprof -http :8000 v5.pprof
Serving web UI on http://localhost:8000

As expected, WorldMap.Neighbours() is the new main bottleneck, simply because it calls WorldMap.Contains() 4 times. Even though there is a branch in it, it probably gets predicted correctly most of the time (as most of the time the particle will not be on the edge of the world) so I’m not sure that is the cause of the slowness. Probably having to fetch 4 values from memory just takes time.

Version 6 - Precompute neighbours

We now spend most of the time in Point.Neighbours(). But what if we could precompute it? In all probability it would be done once and used many times. Let’s try it. Our data structure WorldMap (in worldmap.go), instead of storing a boolean to represent the presence or absence of a point at a location, will store a set of properties of the location:

type locationProps uint8 // Properties of a location on the map

const (
    hasPoint   locationProps = 1 << iota // A point was added here
    isAdjacent                           // A point was added next to here
)

type WorldMap [worldWidth * worldHeight]locationProps

For convenience, let’s have two primitives operate on *WorldMap instances:

func (m *WorldMap) merge(p Point, props locationProps) {
    if p.X < 0 || p.X >= worldWidth || p.Y < 0 || p.Y >= worldHeight {
        return
    }
    m[p.X*worldHeight+p.Y] |= props
}

func (m *WorldMap) get(p Point) locationProps {
    return m[p.X*worldHeight+p.Y]
}

Let’s modify WorldMap.Add() so that it not only marks the point on the map, but also marks all its neighbours as adjacent to a point on the map.

// Add p to the map.
func (m *WorldMap) Add(p Point) {
    m.merge(p, hasPoint)
    m.merge(p.Translate(1, 0), isAdjacent)
    m.merge(p.Translate(-1, 0), isAdjacent)
    m.merge(p.Translate(0, 1), isAdjacent)
    m.merge(p.Translate(0, -1), isAdjacent)
}

Then WorldMap.Contains() and WorldMap.Neighbours() have a very simple implementation:

// Contains returns true if p was added to the map.
func (m *WorldMap) Contains(p Point) bool {
    return m.get(p)&hasPoint != 0
}

// Neighbours returns true if the map contains a point one step away from p.
func (m *WorldMap) Neighbours(p Point) bool {
    return m.get(p)&isAdjacent != 0
}

There is a also a slight adjustment to WorlMap.Add() which is not very interesting so I’ll skip it. Let’s see if that makes a difference.

❯ go run . -cpuprofile v6.pprof
2024/10/17 20:56:42 Worker count: 10
2024/10/17 20:56:42 Points: 1000 - 144.477333ms
2024/10/17 20:56:42 Points: 2000 - 144.657167ms
2024/10/17 20:56:42 Points: 3000 - 212.8675ms
2024/10/17 20:56:42 Points: 4000 - 215.813583ms
[...]
2024/10/17 20:56:45 Points: 297000 - 2.502529958s
2024/10/17 20:56:45 Points: 298000 - 2.503092083s
2024/10/17 20:56:45 Points: 299000 - 2.503448708s
2024/10/17 20:56:45 Points: 300000 - 2.504413792s

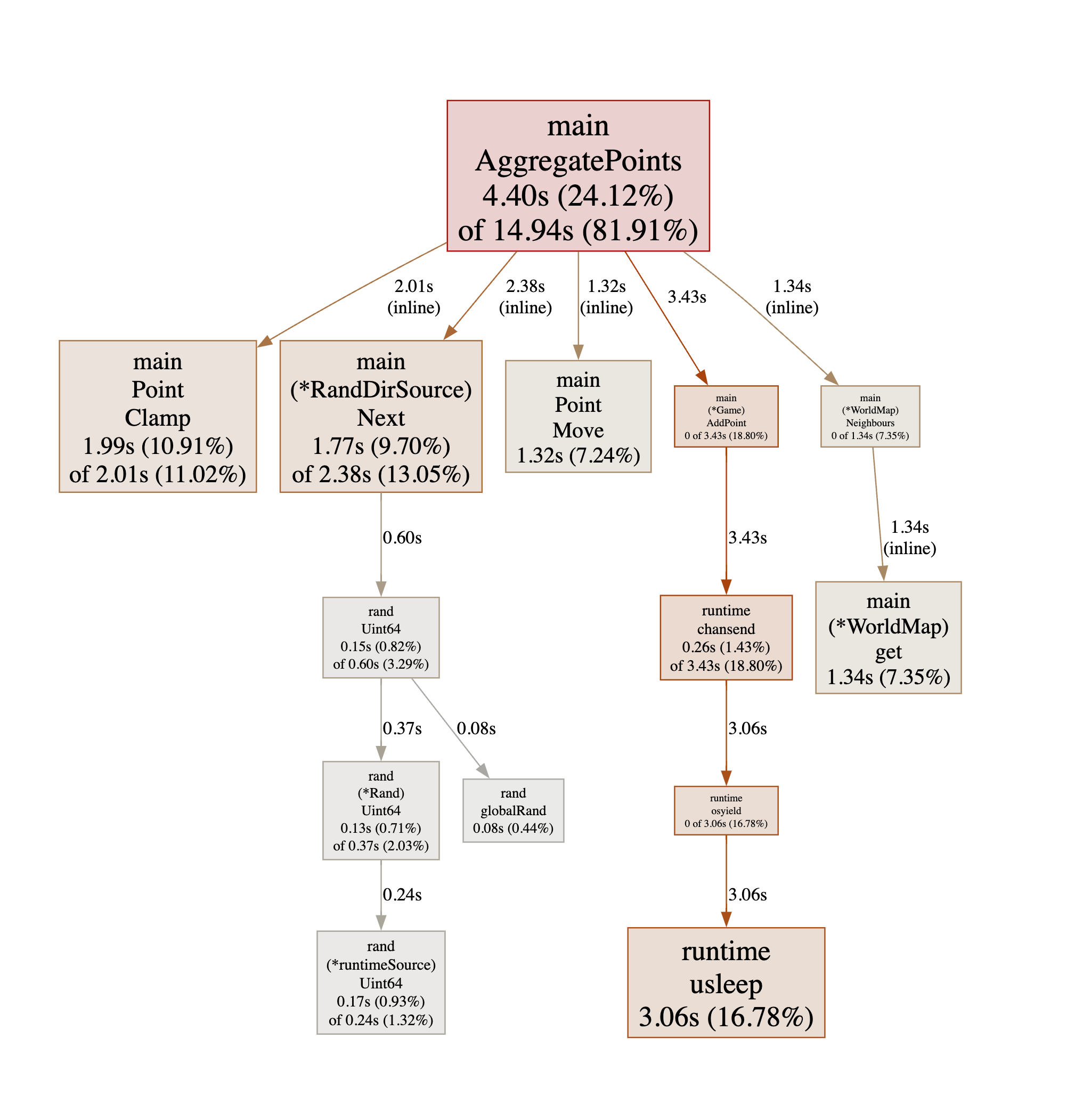
That’s another substantial speedup by a factor of 1.6! As usual, let’s take a look at what pprof tells us.

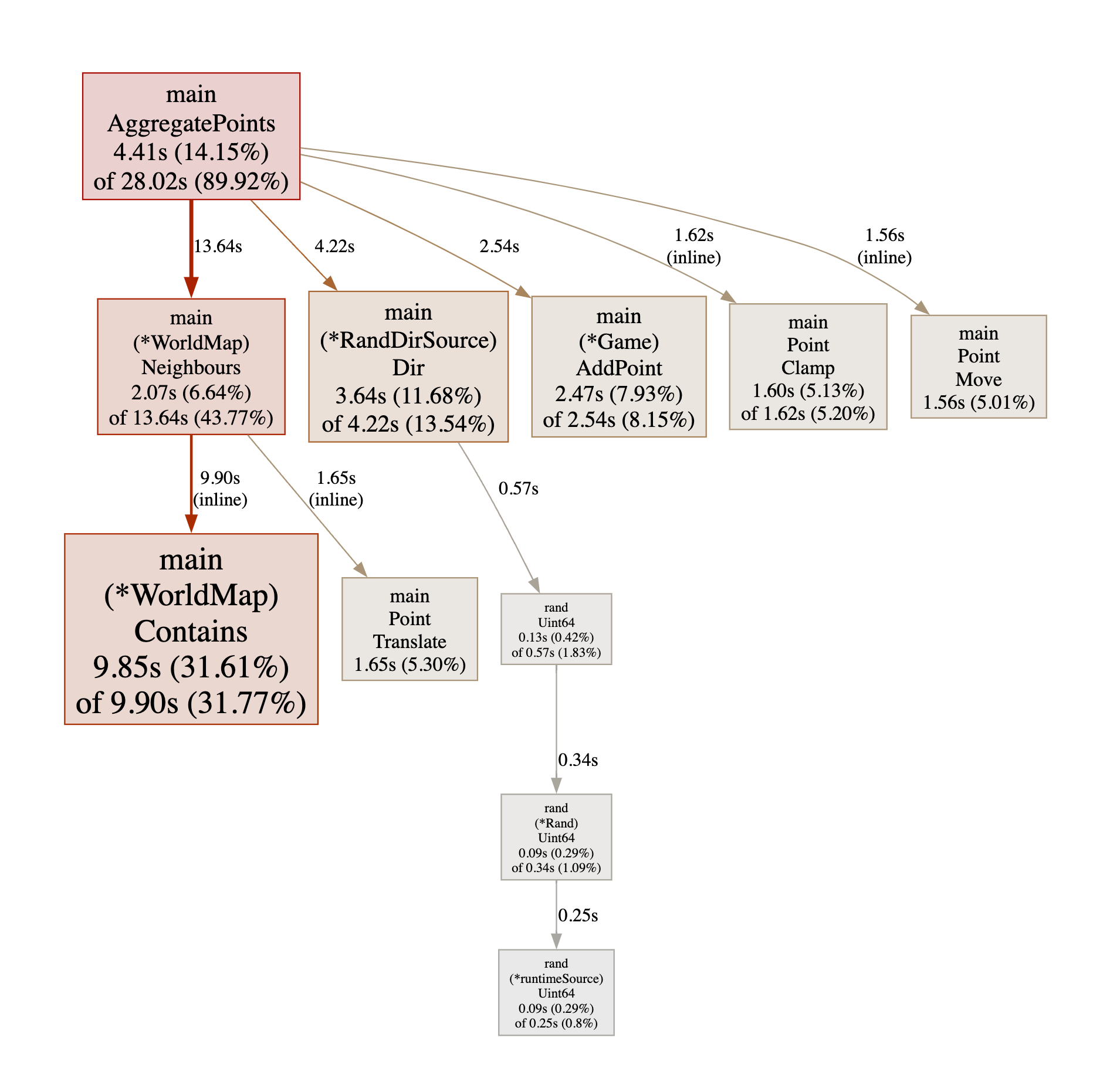
❯ go tool pprof -http :8000 v6.pprof
Serving web UI on http://localhost:8000

For clarity I have removed irrelevant nodes in the graph.

This is interesting - the function inside which most time is spent is (*RandDirSource).Dir() - the graph tells us something else that is interesting: the function is not inlined. So perhaps it is spending a fair amount of time managing the function call?

Note: I was going to try to analyse the disasm output of pprof here, to see if I could find where the time was wasted but I gave up as it proved a bit too hard to interpret the output for me. If I had more time it would be really interesting though, as I think it would be an opportunity to learn about the calling conventions on my platform (darwin/aarch64).

Version 7 - Inline function in hot path by splitting it

There are no easy pickings anymore, but we saw in the previous analysis that the function (*RandDirSource).Dir() is on the hot path and is just too big to be inlined. Would be get a significant speedup by splitting it in two and thus inlining both halves?

First of all, why is it not inlined? We can get the Go compiler to log the decisions it makes about inlining:

❯ go doc cmd/compile
Usage:

    go tool compile [flags] file...

The specified files must be Go source files and all part of the same package.
The same compiler is used for all target operating systems and architectures.
The GOOS and GOARCH environment variables set the desired target.

Flags:
[...]
    -m
        Print optimization decisions. Higher values or repetition
        produce more detail.
[...]

I tried to run go tool compile as a standalone tool, but got problems with import paths that I couldn’t easily resolve, so in the end it was easier to run go build and use the -gcflags option to pass the -m flag to the compiler. Also it turned out you need to repeat the flag to get information about inlining decisions:

❯ go build -gcflags '-m -m' . 2>&1 | grep Dir
./worker.go:43:6: cannot inline (*RandDirSource).Dir: function too complex: cost 90 exceeds budget 80

So close! The Go compiler computes a cost for the compiled function which is sort of proportional to the amount of work done in it. If that cost is more than 80, it won’t inline it. And that’s a final decision as far as I’m aware; there’s no way to make it change its mind. So we could do two things

1. Manually inline the whole function inside AggregatePoints()
2. Change the interface of RandDirSource to have two functions instead of one.

I’m going to go with (2). It is not ideal (there is no reason to do it apart from getting the compiler to inline the code), but still a bit clearer than (1). Our function looks like this:

type RandDirSource struct {
    r uint64
    i int
}

func (s *RandDirSource) Dir() int {
    if s.i == 0 {
        s.i = 32
        s.r = rand.Uint64()
    }
    dir := int(s.r % 4)
    s.i--
    s.r >>= 2
    return dir
}

I’m going to split it like this:

func (s *RandDirSource) Next() {
    if s.i == 0 {
        s.i = 31
        s.r = rand.Uint64()
    } else {
        s.i--
        s.r >>= 2
    }
}

func (s *RandDirSource) Get() int {
    return int(s.r % 4)
}

So d = s.Dir() is the same as s.Next(); d = s.Get(). Let’s check that those function do get inlined now.

❯ go build -gcflags '-m -m' . 2>&1 | grep -E 'Next|Get'
./worker.go:44:6: can inline (*RandDirSource).Next with cost 79 as: method(*RandDirSource) func() { if s.i == 0 { s.i = 31; s.r = rand.Uint64() } else { s.i--; s.r >>= uint(2) } }
./worker.go:54:6: can inline (*RandDirSource).Get with cost 6 as: method(*RandDirSource) func() int { return int(s.r % uint64(4)) }
./worker.go:31:19: inlining call to (*RandDirSource).Next
./worker.go:32:29: inlining call to (*RandDirSource).Get

Yes, just about! And let’s see if that makes a difference.

❯ ./go-dla-v7 -cpuprofile v7.pprof
2024/10/17 22:34:33 Worker count: 10
2024/10/17 22:34:33 Points: 1000 - 163.806959ms
2024/10/17 22:34:33 Points: 2000 - 164.144625ms
2024/10/17 22:34:33 Points: 3000 - 164.232584ms
2024/10/17 22:34:33 Points: 4000 - 164.414209ms
[...]
2024/10/17 22:34:35 Points: 297000 - 2.107752042s
2024/10/17 22:34:35 Points: 298000 - 2.108141709s
2024/10/17 22:34:35 Points: 299000 - 2.108904084s
2024/10/17 22:34:35 Points: 300000 - 2.109414417s

We’re still making visible progress but the speedup factor is starting to slow down, now only 1.2. Nevertheless let’s take a look at what pprof tells us (as usual now I have curated the result a bit).

❯ go tool pprof -http :8000 v7.pprof
Serving web UI on http://localhost:8000

The graph is fairly similar to the one for version 6. The timings seem to move around a bit between AggregatePoints() and the inlined functions it “calls”, but I suspect it’s hard for the profiler to allocate correctly to the caller or the callee when the function is inlined, and the compiled code might end up interleaving the two, so I’m going to put down the fluctuations to that…

The new function RandDirSource.Next() still takes a fair chunk of time, and there is a new kid on the block: runtime.usleep(). That one started making an appearance in version 6 actually, but is creeping up the rankings in version 7. It seems to be called by runtime.chansend, so could it be that the channel that all the workers send their results on is starting to block those worker threads? I’m going to keep that thought and try to find another way to make AggregatePoints() faster. If that makes runtime.usleep() take more time again, then we’ll have to look into that.

The problem is: what is a good candidate for optimisation? We’ve gone through everything more or less, apart from Point.Clamp(). That is interesting, because it takes a significant amount of time, but in the vast majority of cases, it is actually a no-op, as it only does something when we move off the limits of the world. On top of that, it is always executed just after Point.Move(), so perhaps this is something that can be done here.

Version 8 - Speed up hot path by merging two functions

It’s getting hard to see what individual functions can be made faster at this point. In the previous version, we split a function in two. This time, we notice that we execute p.Move(dir).Clamp() on the hot path. Could we merge these two to make the code more efficient?

We currently have

func (p Point) Move(dir int) Point {
    a := dir & 1
    b := dir >> 1
    return Point{
        X: p.X + a - b,
        Y: p.Y + a + b - 1,
    }
}

To clamp the point, we are in a slightly better position than in the Point.Clamp() method, as we know that if the new value of the coordinate is out of bounds, the clamped one is the previous value of the coordinate. Taking advantage of that we can write Point.MoveAndClamp() as follows:

// Move the point by one step (dir is expected to be 0, 1, 2 or 3) and clamp it
// to the confines of the world. It is assumed that the initial value of p is
// within the confines of the world.
func (p Point) MoveAndClamp(dir int) Point {
    a := dir & 1
    b := dir >> 1
    x := p.X + a - b
    y := p.Y + a + b - 1
    if uint(x) < worldWidth {
        // We get to this branch if and only if 0 <= x < worldwidth as if x < 0
        // then uint(x) wraps around to a very big number (bigger than
        // worldWidth)
        p.X = x
    }
    if uint(y) < worldHeight {
        // As above we get to this branch if and only if 0 <= y < worldHeight
        p.Y = y
    }
    return p
}

The potential advantage of the above is that we only need to branch once per coordinate to clamp, as opposed to twice in the general purpose Clamp() function.

❯ ./go-dla-v8 -cpuprofile v8.pprof
2024/10/17 23:13:31 Worker count: 10
2024/10/17 23:13:31 Points: 1000 - 152.554209ms
2024/10/17 23:13:31 Points: 2000 - 152.865ms
2024/10/17 23:13:31 Points: 3000 - 152.947917ms
2024/10/17 23:13:31 Points: 4000 - 153.157834ms
[...]
2024/10/17 23:13:33 Points: 297000 - 1.92379075s
2024/10/17 23:13:33 Points: 298000 - 1.924417084s
2024/10/17 23:13:33 Points: 299000 - 1.924971125s
2024/10/17 23:13:33 Points: 300000 - 1.925503125s

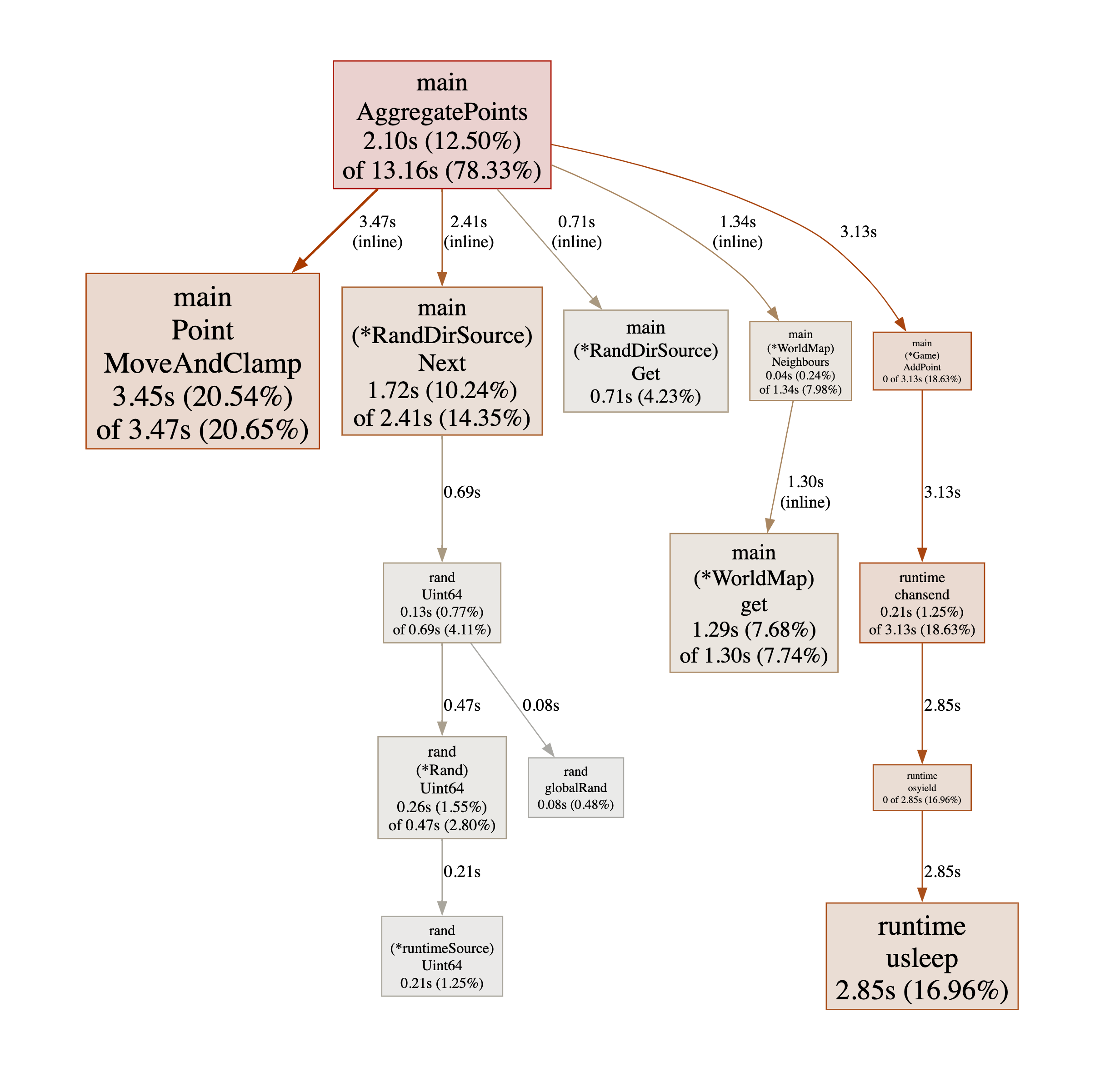
That’s still a significant enough speedup, so it’s a win, but only by a factor of 1.1. Let’s take a look at the pprof output.

❯ go tool pprof -http :8000 v8.pprof
Serving web UI on http://localhost:8000

Let’s take stock.

• Unsurprisingly, Point.MoveAndClamp() becomes the main bottleneck, but we’ve already optimised it as much as we reasonably can, so I think we’re finished here.
• Next there is (*RandDirSource).Next() and (*RandDirSource).Get(). Again we have given them a fair amount of scrutiny and we are no longer wasting any random bits. Both functions are inlined and the data structure is on the stack (TODO: explain how you can tell that) so they are probably as fast as they can be.
• The next one is (*WorldMap).Neighbours(). We are precomputing all neighbouring locations, so it is just a table lookup and I can’t think of much more to do.
• The last one is interesting: (*Game).AddPoint. This gets called every time we have aggregated a point on the map. it is not inlined but that’s fine because it is not on the hot path. However, when it is called, it sends a point on the channel used to communicate with the event loop and it seems to be waiting for a significant amount of time.

Reflecting on the above, I can see to possible avenues for possible improvements:

1. See if we can reduce the time the worker is waiting to send a point on the channel.
2. As all the rest is on the hot path, which consists of moving a point frantically until it aggregates, find a way to do this more efficiently. For example, we could try moving the point by many steps in one go instead of one step at a time. That would help a lot, especially at the start when the world is mostly empty.

In fact, I realise that I haven’t tried to count how many steps the workers have to go through. Let’s make a slight modification to the program to do that and run it.

❯ go run .
2024/10/19 13:08:49 Worker count: 10
2024/10/19 13:08:49 Points: 10000 - Steps = 1170914207, 407.984292ms
2024/10/19 13:08:49 Points: 20000 - Steps = 2204129394, 700.103292ms
2024/10/19 13:08:50 Points: 30000 - Steps = 3022195892, 933.879542ms
2024/10/19 13:08:50 Points: 40000 - Steps = 3685738735, 1.135259917s
[...]
2024/10/19 13:08:51 Points: 270000 - Steps = 5703069540, 1.920117625s
2024/10/19 13:08:51 Points: 280000 - Steps = 5703491443, 1.925909458s
2024/10/19 13:08:51 Points: 290000 - Steps = 5703822539, 1.937591667s
2024/10/19 13:08:51 Points: 300000 - Steps = 5704064762, 1.943454167s

So that’s a grand total of $5,704,064,762$! The program moved $300,000$ particles by $5.7$ billion steps in $1.9$ seconds. It doesn’t sound too bad when you put it like that. That’s more than $2.9$ billion steps per second. Another way to look at it is to say that each step took an average of $3.4\times 10^{-10}s$, or $0.34$ nanoseconds.

So finding a way to execute many steps at once might be the only way to make significant performance improvements.

Mathematical interlude: combinatorics on random walks

At this point I have more or less ran out of optimisations, so I consider the mathematics of random walks, to see if they have properties that may mean we can have a more efficient algorithm for our problem. My aim is to see if it’s possible to generate cheaply a random walk with $N$ steps instead of a single step at a time.

2D random walks

Let’s investigate 2D random walks.

Some definitions

We call a step in $n$ dimensions a non-zero vector in $\Z^n$ with minimal length. Let’s call $\Steps{n}$ the set of all steps in $n$ dimensions. For example

• $\Steps{1} = \{-1, 1\}$
• $\Steps{2} = \{(0, -1), (0, 1), (-1, 0), (1, 0)\}$

A walk in $n$ dimensions is simply a sequence of steps in $n$ dimensions. Given Let’s call $\Walks{n}^N$ the set of all walks in $n$ dimenstions of length $N$. We will call such walks $N$-walks in $n$ dimensions. It is evident that

$$\Walks{n}^N \equiv (\Steps{n})^N$$

Now given a walk $w \in \Walks{n}^N, w = (\vect{s}_i)_{i < N}$, let’s call the destination $\delta(w)$ of $w$ the vector in $\Z^N$ which is the sum of all the steps that compose $w$. In mathematical notation that means

$$\delta(w) = \sum_{i < N} \vect{s}_i$$

Finally, given a vector $\vect{u} \in \Z^n$ we will call $\Walks{\vect{u}}^N$ the set of $N$-walks with destination $\vect{u}$.

$$\Walks{\vect{u}}^N = \setof{ w \in \Walks{n}^N}{\delta(w) = \vect{u}}$$

So for example

• $\Walks{1}^3 = \{ \langle 1, 1, -1\rangle, \langle 1, -1, 1\rangle, \langle -1, 1, 1\rangle \}$
• $\Walks{2}^3 = \emptyset$
• $\Walks{1, 1}^2 = \{ \langle(1, 0), (0, 1)\rangle, \langle(0, 1), (1, 0)\rangle \}$

Our purpose is to calculate the cardinality of $\Walks{x, y}^N$ for any, $x, y \in\Z$. This way we should be able to draw at random a walk in 2 dimensions with $N$ steps. So let’s define

$$W_\vect{u}^N = \left|\Walks{\vect{u}}^N\right|$$

In the rest of this section we will try to calculate $W_\vect{u}^N$ for any $\vect{u}\in\Z^n$.

Concatenating walks in n dimensions (optional)

This subsection is trying to formalise mathematically some ideas which are only used in a very simple context later. I’m keeping it here but it can safely be skipped.

Given two walks in $n$ dimensions $w_1$ and $w_2$ we can define $w_1 \wedge w_2$ to be the walk made by concatenating $w_1$ and $w_2$.

It is fairly obvious that the following identity holds for all walks in $n$ dimensions $w_1$ and $w_2$.

$$\delta(w_1 \wedge w_2) = \delta(w_1) + \delta(w_2)$$

We can extend the $\wedge$ notation to sets. If $A$ and $B$ are sets of walks in $n$ dimensions, then let’s define

$$A \wedge B = \setof{ w_1 \wedge w_2}{w_1 \in A \textrm{ and } w_2 \in B}$$

We have the following

$$\begin{align} (A \wedge B)_\vect{u} & = \setof{w_1 \wedge w_2}{w_1 \in A, w_2 \in B, \delta(w_1 \wedge w_2) = \vect{u} } \notag \\ & = \setof{ w_1 \wedge w_2}{w_1 \in A, w_2 \in B, \delta(w_1) + \delta(w_2) = \vect{u} } \notag \\ & = \bigcup_{u_1 + u_2 = \vect{u}} \setof{ w_1 \wedge w_2 }{ w_1 \in A_{\vect{u} _1}, w_2 \in B_{\vect{u} _2} } \notag \\ & = \bigcup_{u_1 + u_2 = \vect{u}} A_{\vect{u}_1} \wedge B_{\vect{u}_2} \end{align}$$

Let’s apply the above identity to $A = \Walks{n}^N$ and $B = \Walks{n}^M$ (in other words, $A$ is the set of all $N$-words and $B$ is the set of all $M$-words).

$$\begin{equation*} \left(\Walks{n}^N \wedge \Walks{n}^M\right)_\vect{u} = \bigcup_{\vect{u}_1 + \vect{u}_2 = \vect{u}} \Walks{\vect{u}_1}^N \wedge \Walks{\vect{u}_2}^M \end{equation*}$$

On the left-hand side of the above it is evident that $\Walks{n}^N \wedge \Walks{n}^M = \Walks{n}^{N + M}$ and that . Therefore, as $\left(\Walks{n}^{N + M}\right)_u = \Walks{\vect{u}}^{N + M}$,

$$\begin{equation} \Walks{u}^{N + M} = \bigcup_{\vect{u}_1 + \vect{u}_2 = \vect{u}} \Walks{\vect{u}_1}^N \wedge \Walks{\vect{u}_2}^M \end{equation}$$

On the right-hand side, it is easy to prove that the union is disjoint. Let’s imagine that $w \in \Walks{\vect{u}_1}^N \wedge \Walks{\vect{u}_2}^M \cap \Walks{\vect{u}'_1} \wedge \Walks{\vect{u}'_2}$ with $(\vect{u}_1, \vect{u}_2) \neq (\vect{u}'_1, \vect{u}'_2)$ and find a contradiction. Then $w = w_1 \wedge w_2 = w'_1 \wedge w'2$ with $w_1 \in \Walks{u_1}^N$ and $w'_1 \in \Walks{u'_1}^N$. That is only possible if $w_1 = w'_2$, which means $\delta(w_1) = \delta(w_2)$, therefore $\vect{u}_1 = \vect{u}_2$ which contradict our premise. So we infer from $(2)$ that

$$\begin{align*} \left|\Walks{u}^{N + M}\right| & = \left|\bigcup_{\vect{u}_1 + u_2 = u} \Walks{\vect{u}_1}^N \wedge \Walks{\vect{u}_2}^M\right| & \\ W_\vect{u}^{N + M} & = \sum_{\vect{u}_1 + \vect{u}_2 = \vect{u}} \left|\Walks{\vect{u}_1}^N \wedge \Walks{\vect{u}_2}^M\right| \end{align*}$$

On the right-hand side, to calculate the cardinality of each set, let’s remark that the following mapping is a bijection.

$$\begin{align*} p: \Walks{\vect{u}_1}^N \times \Walks{\vect{u}_2}^M & \longrightarrow \Walks{\vect{u}_1}^N \wedge \Walks{\vect{u}_2}^M \\ (w_1, w_2) & \longmapsto w_1 \wedge w_2 \end{align*}$$

Therefore $\left|\Walks{\vect{u}_1}^N \wedge \Walks{\vect{u}_2}^M\right| = W_{\vect{u}_1}^N W_{\vect{u}_2}^M$. Thus we obtain the following identity.

$$\begin{equation} W_\vect{u}^{N + M} = \sum_{\vect{u}_1 + \vect{u}_2 = \vect{u}} W_{\vect{u}_1}^N W_{\vect{u}_2}^M \end{equation}$$

One thing that we can do is set $M = 1$, which gives us the following recurrence relation.

$$\begin{equation} W_{\vect{u}}^{N + 1} = \sum_{\vect{v} + \vect{s} = \vect{u}} W_{\vect{v}}^N= \sum_{s\in \Steps{n}} W_{\vect{u} - \vect{s}}^N \end{equation}$$

The number of walks in 1 dimension

If we take $n = 1$ in identity $(4)$, given that $\Steps{1} = \{ -1, 1\}$, the recurrence relation becomes as follows.

$$\begin{equation} W_x^{N + 1} = W_{x - 1}^{N} + W_{x + 1}^{N} \end{equation}$$

Note than none of the section above was really needed to come up with this identity, as it essentially says that walks to $x$ in $N + 1$ steps are of two kinds:

• walks to $x - 1$ in $N$ steps followed by a $+1$ step
• walks to $x - 1$ in $N$ steps followed by a $-1$ step

We have a recurrence relation, now we need to know what happens when $N = 0$ an that’s fairly obvious: $W_x^0 = 1$ if $x = 0$, otherwise $W_x^0 = 0$. Armed with this, let’s calculate a few values step by step.

$$\def\arraystretch{1.5} \begin{array}{c:c:c:c:c:c:c:c} x & -3 & -2 & -1 & \;0\; & \;1\; & \;2\; & \;3\; \\ \hline W_x^0 & 0 & 0 & 0 &1 & 0 & 0 & 0 \\ W_x^1 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ W_x^2 & 0 & 1 & 0 & 2 & 0 & 1 & 0 \\ W_x^3 & 1 & 0 & 3 & 0 & 3 & 0 & 1 \end{array}$$

That looks slightly familiar! First let’s deal with the zeroes. We will prove the following by induction on $N$

$$W_x^N = 0 \textrm{ if } N + x \equiv 1 (\bmod 2) \textrm{ for all } N \in \N$$

• It is true when $N=0$ as $W_x^0 = 0$ for all $x \neq 0$.
• If it is true for $N$, then let $x$ be such that $(N + 1) + x \equiv 1 (\bmod 2)$. Then $N + (x + 1) \equiv 1 (\bmod 2)$ and $N + (x - 1) \equiv 1- 2 \equiv 1 (\bmod 2)$. Therefore $W_{x - 1}^N = 0$ and $W_{x + 1}^N = 0$ and by the recurrence relation, it follows that $W_x^{N+1} = 0$.

Let’s now look at the other values, Let $x\in\Z$ such that $N - x \equiv 0 (\bmod 2)$. There is $k\in\Z$ such that $N - x = 2k$, or equivalently $x = N - 2k$. Let’s define

$$Z_k^N = W_{N - 2k}^N$$

Let’s try to calculate $Z_k^{N + 1}$.

$$\begin{align*} Z_k^{N+1} & = W_{N+1 - 2k}^{N+1} \\ & = W_{N - 2k}^N + W_{N + 2 - 2k}^N \\ & = Z_k^N + W_{N - 2(k - 1)}^N \\ & = Z_k^N + Z_{k - 1}^N \end{align*}$$

Therefore we have

$$\begin{cases} Z_0^0 = 1 \\ Z_k^0 = 0 & \textrm{for } k \neq 0 \\ Z_k^{N+1} = Z_k^N + Z_{k - 1}^N & \textrm {for } N \geq 0. \end{cases}$$

This means that $Z_k^N = C_k^N$, the number of $k$-combinations of a set with $N$ elements. It’s not surprising really, given that we saw Pascal’s triangle appear earlier on. If we go back to the number of walks, we get the following identity.

$$W_x^N = C_k^N \textrm{ where } N - x = 2k \textrm{ if } N - x \equiv 0 (\bmod 2)$$

So to summarise, we have proved that for any $N\in\N$

$$\begin{equation} W_x^N = \begin{cases} C_k^N \textrm{ where } x = N - 2k & \textrm{if } x \equiv N (\bmod 2) \\ 0 & \textrm{otherwise} \end{cases} \end{equation}$$

The number of walks in 2 dimensions

Can we use similar tactics to calculate the number of walks in 2 dimensions? Possibly, but I stared at $(4)$ and $(5)$ for a bit but couldn’t find a way to use them.

Instead I got a breakthrough by taking a different approach, and reducing the problem to what we’ve already solved: 1-dimensional walks.

To prove it mathematically I prefer to take a step back and consider a more general situation.

Given a $\Z$-module $U$ and a positive integer $n$, there is a natural homomorphism

$$\begin{align*} \delta: U^n & \longrightarrow U \\ (x_1, \dots, x_n) & \longmapsto \sum_{i=1}^n x_i \end{align*}$$

Let’s consider another $\Z$-module $V$, and a monomorphism $f: U \rightarrow V$. Let’s also have a subset $S$ of $U$.

Then $f$ induces a monomorphism

$$\begin{align*} f^n: U^n & \longrightarrow V^n \\ (x_1, \dots, x_n) & \longmapsto (f(x_1), \dots, f(x_n)) \end{align*}$$

It is easy to verify that $\delta f(x) = f\delta(x)$:

$$\begin{align*} \delta f^n(x_1, \dots, x_n) & = \delta(f(x_1), \dots, f(x_n)) \\ & = \sum_{i=1}^n f(x_i) \\ & = f\left(\sum_{i=1}^n x_i\right) \\ & = f(\delta(x_1, \dots, x_n)). \end{align*}$$

Therefore we can draw the following commutative diagram where the horizontal arrows are monomorphisms.

$$\begin{CD} U^n @> f^n >> V^n \\ @V \delta VV @V \delta VV \\ U @> f >> V \end{CD}$$

Let $S$ be a subset of $U$, then from the diagram above we infer the following commutative diagram where the horizontal arrows are bijective.

$$\begin{CD} S^n @> f^n >> f(S)^n \\ @V \delta VV @V \delta VV \\ S @> f >> f(S) \end{CD}$$

Now let $U = \Z^2$, $V = \Z\times\Z$, $n = N$, $f(x, y) = (x + y, x - y)$ and $S = \Steps{2}$. It is straigthforward to verify that $f$ is a monomorphism.

First of all, $\Steps{1}^N = \Walks{1}^N$. Also, $f(\Steps{2}) = \{(1, 1), (-1, -1), (1, -1), (-1, 1)\} = \Steps{1}\times\Steps{1}$, so the above commutative diagram turns into the following.

$$\begin{CD} \Walks{2}^N @> f^N >> (\Steps{1}\times\Steps{1})^N \\ @V \delta VV @V \delta VV \\ \Steps{2} @> f >> \Steps{1}\times\Steps{1} \end{CD}$$

There is a natural isomorphism

$$\begin{align*} \sigma: (\Z\times\Z)^N & \longrightarrow \Z^N \times \Z^N \\ ((x_1, y_1), \dots, (x_N, y_N)) & \longmapsto ((x_1, \dots, x_N), (y_1, \dots, y_N)) \end{align*}$$

Given that $\sigma((\Steps{1}\times\Steps{1})^N) = \Steps{1}^N\times\Steps{1}^N$ and $\Steps{1}^N = \Walks{1}^N$ this allows us to draw the following comutative diagram (I haven’t proved that the right-hand side is commutative but it’s quite obvious).

$$\begin{CD} \Walks{2}^N @> f^N >> (\Steps{1}\times\Steps{1})^N @> \sigma >> \Walks{1}^N \times \Walks{1}^N \\ @V \delta VV @V \delta VV @V \delta\times\delta VV \\ \Steps{2} @> f >> \Steps{1}\times\Steps{1} @= \Steps{1}\times\Steps{1} \end{CD}$$

In this diagram, all the horizontal arrows are all bijective. This means that $\sigma f^N$ is a bijection from $\Walks{2}^N$ to $\Walks{1}^N \times \Walks{1}^N$. Now let’s pick $w$, an $N$-walk in 2 dimensions with destination $(x, y)$ and let $(w1, w2) = \sigma f^N(w)$. Both $w_1$ and $w_2$ are $N$ walks in 1 dimension and from the commutativity of the diagram above, we know that $(\delta(w_1), \delta(w_2)) = f(x, y) = (x + y, x - y)$. This means that $\delta(w_1) = x + y$ and $\delta(w_2) = x - y$.

We can reword the above as follows.

Theorem 1. There is a bijection between $\Walks{2}^N$ and $\Walks{1}^N \times \Walks{1}^N$ matching walks in 2 dimensions with destination $(x, y)$ with pairs of walks in 1 dimension with destination $x + y$ and $x - y$.

It follows from this that $W_{x, y}^N = W_{x + y}^N W_{x - y}^N$ and as we calculated the number of $N$-walks in 1 dimensions in the previous section, we can now provide a formula for the number of $N$-walks in 2 dimensions.

$$\begin{equation} W_{x, y}^N = \begin{cases} C_k^N C_l^N \textrm{ where } \begin{cases} x + y = N - 2k \\ x - y = N - 2l \end{cases} & \textrm{if } N \equiv x + y (\bmod 2) \\ 0 & \textrm{otherwise} \end{cases} \end{equation}$$

Version 9 - Use the power of Maths!

Remember after version 8 I concluded that it would be difficult to optimise the current algorithm any further and that one way to go faster would be to move several steps at once. So let’s simplify the problem for a moment and imagine that we are far enough from any existing points on the map, so that there is no danger of aggregating if we move by $N$ steps in one go.

We need to find an efficient way to calculate the destination of a random $N$-walk $w$ in 2 dimensions. Let’s call $(x, y) = \delta(w)$ this destination. According to theorem 1, this is equivalent to generating two random $N$-walks $w_1$ and $w_2$ in one dimension. and then solving the following system for $x$ and $y$.

$$\begin{equation*} \begin{cases} x + y & = \delta(w_1) \\ x - y & = \delta(w_2) \end{cases} \end{equation*}$$

But according to $(6)$

• $\delta(w_1) = N - 2k$ where $k$ is a randomly generated value from the binomial distribution $B(N, \frac{1}{2})$.
• $\delta(w_2) = N - 2l$ where $l$ is a randomly generated value from the binomial distribution $B(N, \frac{1}{2})$.

So we generate two values $k, l$ at random from $B(N, \frac{1}{2})$ and solve the following system.

$$\begin{equation*} \begin{cases} x + y & = N - 2k \\ x - y & = N - 2l \end{cases} \end{equation*}$$

Adding the equations gives us $2x = 2N - 2k - 2l$ and subtracting them gives us $2y = 2l - 2k$, which we can sum up as

Theorem 2. A random $N$-walk in 2 dimension has destination $(x, y) = (N - k - l, l - k)$ where $k$ and $L$ are randomly sampled from the binomial distribution $B(N, \frac{1}{2})$.

The last problem to solve is how to sample efficiently from the binomial distribution $B(N, \frac{1}{2})$. This is equivalent to tossing $N$ coins and counting the number of heads, or to generating $N$ random bits and counting the number of ones.

Well, generating random bits is easy, we can do it 64 at a time. As for counting the ones, the Go standard library provides us with the math/bits package to do this kind of thing - look at OnesCount and friends. So we have everything to implement it. We’ll assume we won’t want to do more than 32 steps at a time, so that 64 bits is enough randomness to calculate the displacement of the walk.

// Find in one go the displacement (x, y) after N random steps of a 2D random
// walk.
//
// N is a constant integer, 1 <= N <= 32 (32 because we need 2N random bits
// from a total of 64 bits).
func RandomFreeWalk() (x int, y int) {
    const N = freeWalkSize // We'll define this in constants.go
    r := rand.Uint64()
    // Select N bits from the lower 32 bits and count the ones
    k := bits.OnesCount32(uint32(r << (32 - N)))
    // Select N bits from the higher 32 bits and count the ones
    l := bits.OnesCount32(uint32(r >> (64 - N)))

    x = N - k - l
    y = l - k
    return
}

It’s amazing that after all this maths, we end up with such a simple implementation!

We can’t always use this RandomFreeWalk function - only when there isn’t already a point on the map within $N$ steps of the current position. Ok le’ts imagine for a moment that we have a method that allows us to answer that question.

// CannotFreeWalkFrom returns true if there is an obstacle nearby preventing a
// free walk from p.
func (m *WorldMap) CannotFreeWalkFrom(p Point) bool {
    // TODO: implement this
}

We can modify AggregatePoints to jump by $N$ steps in one go as long as it is safe, as follows.

func AggregatePoints(
    workerNumber int,
    worldMap *WorldMap,
    pickPoint func() Point,
    addPoint func(Point, int),
) {
    var randDirSrc RandDirSource
    for {
        p := pickPoint()
        i := 0
        for worldMap.Contains(p) {
            i++
            if i == 100 {
                log.Printf("Worker %d stopping", workerNumber)
                return
            }
            p = pickPoint()
        }
        steps := 0
        // ------- New part starts here --------
        for !worldMap.CannotFreeWalkFrom(p) {
            p = p.Translate(RandomFreeWalk()).Clamp()
            steps += freeWalkSize
        }
        // ------- New part ends here ----------
        for !worldMap.Neighbours(p) {
            randDirSrc.Next()
            p = p.MoveAndClamp(randDirSrc.Get())
            steps++
        }
        worldMap.Add(p)
        addPoint(p, steps)
    }
}

Now to implement (*WorldMap).CannotFreeWalkFrom(), let’s use the same idea that we did for implementing (*WorldMap).Neighbours(). Whenever we add a point to the map, we update the points in the vicinity with a flag indicating that there is a point within reach of $N$ steps as follows.

func (m *WorldMap) Add(p Point) {
    m.merge(p, hasPoint)
    m.merge(p.Translate(1, 0), isAdjacent)
    m.merge(p.Translate(-1, 0), isAdjacent)
    m.merge(p.Translate(0, 1), isAdjacent)
    m.merge(p.Translate(0, -1), isAdjacent)
    // -------- New part: mark points within reach as `cannotFreewalk`
    var jMax int
    for i := -freeWalkSize; i <= freeWalkSize; i++ {
        if i < 0 {
            jMax = freeWalkSize + i
        } else {
            jMax = freeWalkSize - i
        }
        for j := -jMax; j <= jMax; j++ {
            m.merge(p.Translate(i, j), cannotFreeWalk)
        }
    }
}


// CannotFreeWalkFrom returns true if there is an obstacle nearby preventing a
// free walk from p.
func (m *WorldMap) CannotFreeWalkFrom(p Point) bool {
    return m.get(p)&cannotFreeWalk != 0
}

The constant cannotFreeWalk needs to be added to the list of locationProps in the same file.

const (
    hasPoint locationProps = 1 << iota // A point was added here
    isAdjacent
    cannotFreeWalk
)

Lastly we need to decide the value of freeWalkSize, which must be at most 32. I have experimented with different values and it seems like 16 work quite well. I guess if the value is too big, it can no longer be used when the gaps become small, and if it is too small it doesn’t offer a significant advantage over moving by individual steps.

Another value that I have adjusted is maxPendingPoints. As this version is becoming very fast, the channel storing pending points was filling up before the game loop could consume it and it was making the worker goroutines spend too long waiting on the channel. I have increased that to 20000 so the new constants are as follows.

const (
    worldWidth  = 1000
    worldHeight = 1000

    maxPendingPoints = 20000

    // Size of a "free walk" - a walk that we can perform in one go because
    // there are no obstacles within that number of steps.  It must be at most
    // 32.
    freeWalkSize = 16
)

Let’s run it!

❯ go run . -cpuprofile v9.pprof
2024/10/27 21:44:22 Worker count: 10
2024/10/27 21:44:22 Points: 10000 - Steps = 1189839249, 133.712ms
2024/10/27 21:44:22 Points: 20000 - Steps = 2201331477, 238.655458ms
2024/10/27 21:44:23 Points: 30000 - Steps = 3042106230, 337.4275ms
2024/10/27 21:44:23 Points: 40000 - Steps = 3723221259, 404.22225ms
[...]
2024/10/27 21:44:23 Points: 270000 - Steps = 5525374603, 836.539125ms
2024/10/27 21:44:23 Points: 280000 - Steps = 5525894231, 856.894541ms
2024/10/27 21:44:23 Points: 290000 - Steps = 5526288504, 863.957208ms
2024/10/27 21:44:23 Points: 300000 - Steps = 5526626308, 873.307875ms```

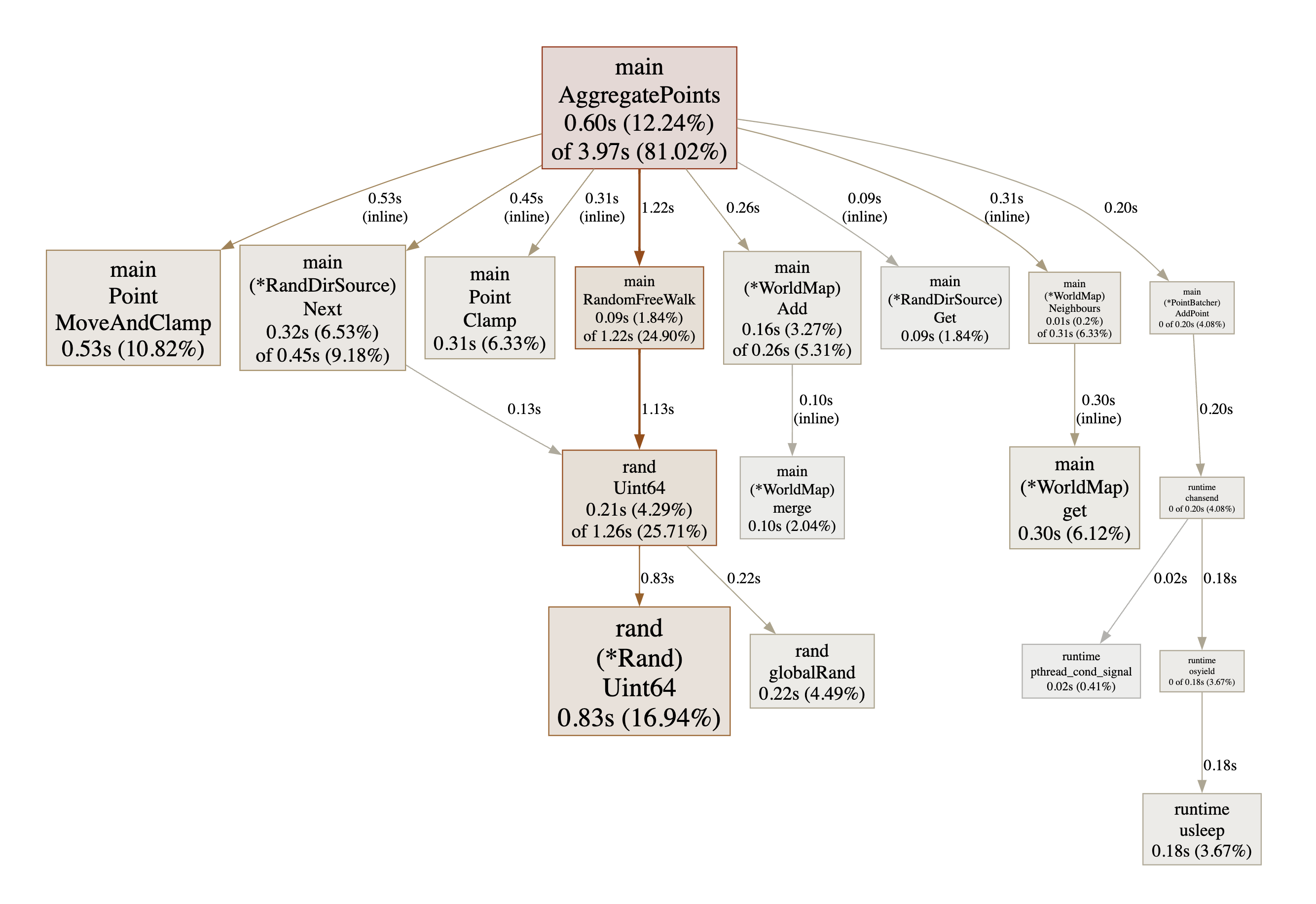
So we got 873ms, that is a speedup by a factor of almost 2.2! And we got under 1s, which is what I was secretly hoping for… Ok, let’s take a look at pprof.

❯ go tool pprof -http :8000 v8.pprof
Serving web UI on http://localhost:8000

As I was hoping, a lot of pressure has been removed from the Point.MoveAndClamp() method which was heavily optimised. But now, probably because points are generated so fast by the workers, contention for sending on the pending channel is becoming very significant. Is there anything that we can do about this? This is going to be the next point of focus - and the last one, I promise!

Version 10 - just one more thing!

If in version 9 the workers are spending too much time waiting to send a point on the game loop’s pending points channel, then let’s make them send fewer things on that channel. How can we do that? An obvious way is to send batches of points instead of individual points. Let’s do it in a parametrised way. We’re going to add a batchSize constant and do everything in terms of it.

const batchSize = 20

We need to adapt the game loop so it maintains a channel of batches of points instead of individual points. Fortunately we already have pendingItem data structure. Let’s change it to this.

type pendingItem struct {
    points [batchSize]Point
    steps  int
}

In NewGame we’re going to keep the number of pending points the same so we’ll change the buffer size of the channel to maxPendingPoints/batchSize.

func NewGame(initialPoints iter.Seq[Point], maxPoints int) *Game {
    game := &Game{
        worldImage: ebiten.NewImage(worldWidth, worldHeight),
        pending:    make(chan pendingItem, maxPendingPoints/batchSize),
        maxPoints:  maxPoints,
    }
    ...
}

And then in the game loop, when we receive a pending item, we now need draw all the points in it. This means we change the (*Game).Update() function’s case item := <-g.pending as follows.

        case item := <-g.pending:
            for _, p := range item.points {
                // Start white and gradually fade out to black
                g.worldImage.Set(
                    p.X, p.Y,
                    color.Gray16{Y: uint16(0xFFFF * (n - i) / n)},
                )
            }
            s += item.steps
            i += batchSize
            if i%10000 < batchSize {
                log.Printf("Points: %d - Steps = %d, %s", i, s, time.Since(g.start))
            }
            if i >= n {
                pprof.StopCPUProfile()
                return nil
            }

Last thing, we don’t need an AddPoint() method but rather an AddBatch() one.

// AddBatch adds a batch of points to the pending items
func (g *Game) AddBatch(points *[batchSize]Point, steps int) {
    g.pending <- pendingItem{
        points: *points,
        steps:  steps,
    }
}

That’s it for the game loop!

Now we’ll create an adapter type for AggregatePoints so it can still only be concerned with adding individual points.

// PointBatcher accumulates points to send to the game loop as a batch, so
// others doon't have to worry about doing that.
type PointBatcher struct {
    game   *Game
    points [batchSize]Point
    steps  int
    i      int
}

func newPointBatcher(game *Game) *PointBatcher {
    return &PointBatcher{game: game}
}

// AddPoint adds a point to the batcher, possibly triggering sending a batch to
// its game if the batch size has been reached.
func (b *PointBatcher) AddPoint(p Point, steps int) {
    b.points[b.i] = p
    b.steps += steps
    b.i++
    if b.i == batchSize {
        b.game.AddBatch(&b.points, b.steps)
        b.i = 0
        b.steps = 0
    }
}

All that remains to be done is to create a *PointBatcher for each worker so it can use it to send points, that’s done in the main() function.

func main() {
    ...
    for i := 1; i <= workerCount; i++ {
        batcher := newPointBatcher(game)
        go AggregatePoints(i, worldMap, method.pickPoint, batcher.AddPoint)
    }
    ...
}

We’re done! Let’s hope it works. Note: I’ve experimented with various batch sizes, but it looks like 20, which was really my first guess, is a pretty good value.

❯ go run . -cpuprofile v10.pprof
2024/10/27 22:13:47 Worker count: 10
2024/10/27 22:13:47 Points: 10000 - Steps = 1161799448, 168.772167ms
2024/10/27 22:13:47 Points: 20000 - Steps = 2185878426, 255.932708ms
2024/10/27 22:13:47 Points: 30000 - Steps = 2997724177, 330.172958ms
2024/10/27 22:13:47 Points: 40000 - Steps = 3624112404, 404.131542ms
[...]
2024/10/27 22:13:47 Points: 270000 - Steps = 5394107093, 680.045208ms
2024/10/27 22:13:47 Points: 280000 - Steps = 5394488513, 682.787292ms
2024/10/27 22:13:47 Points: 290000 - Steps = 5394813846, 685.154083ms
2024/10/27 22:13:47 Points: 300000 - Steps = 5395066382, 687.178875ms

It was worth it as we sped it up by a factor of almost 1.3.

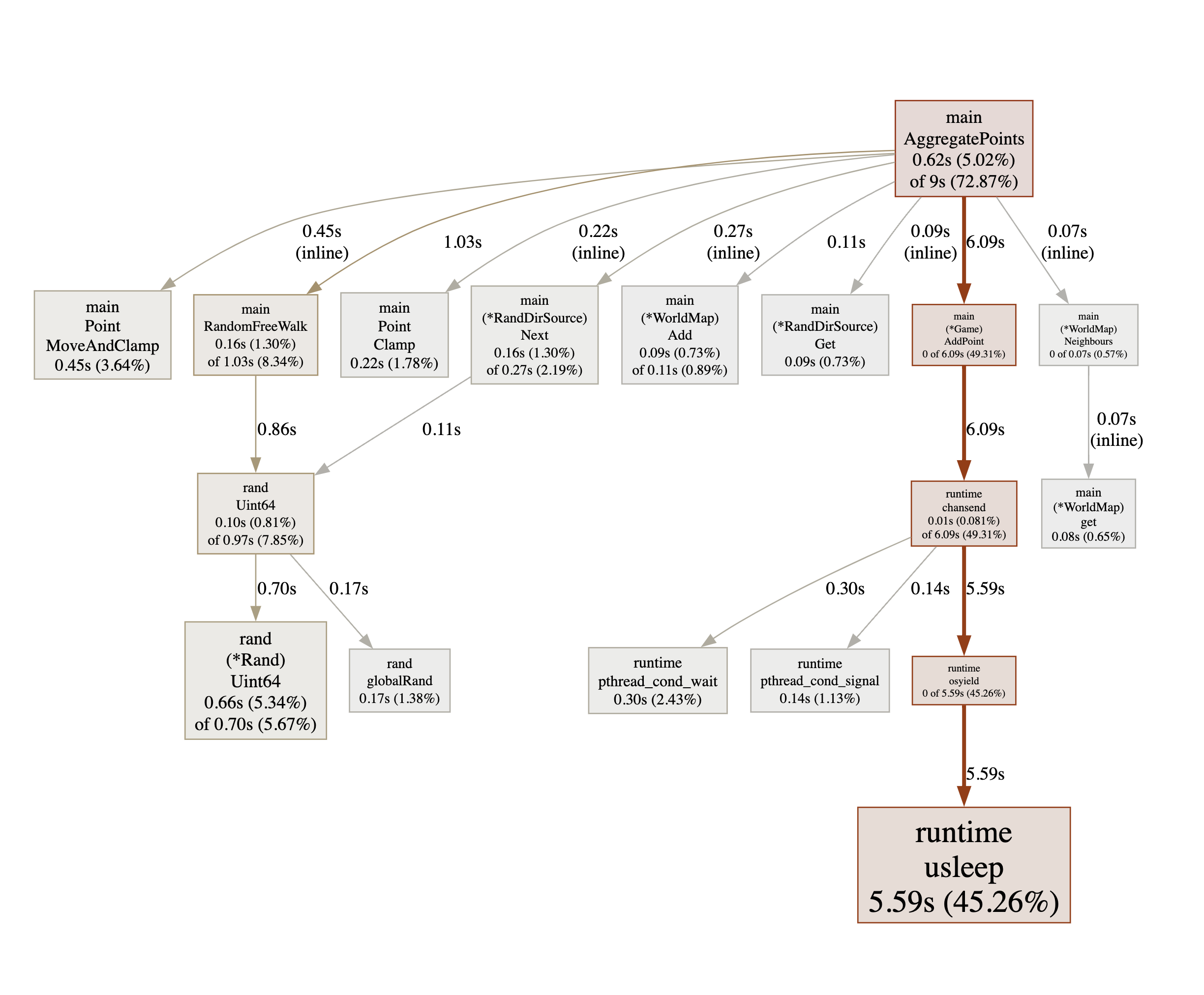
❯ go tool pprof -http :8000 v10.pprof
Serving web UI on http://localhost:8000

This profile shows the batching did its job - the workers are no longer spending any significant time waiting to send a point on the channel. Instead, it’s random generation which is back as the main bottleneck. That makes sense as RandomFreeWalk is burning through random bits pretty fast. Perhaps it would actually be possible to do something about it as currently we set the free walk length to 16 steps, we we could actually do 2 free walks with one 64 bit random number… Actually, I’ve tried it and it doesn’t bring any significant speedup.

So that’s the end of the story! Hope you enjoyed it if you got this far…

Failed attempts

• Using float64 as point coordinates (with the hope of speeding up clamping)
• Making the receiver of MoveAndClamp() a pointer